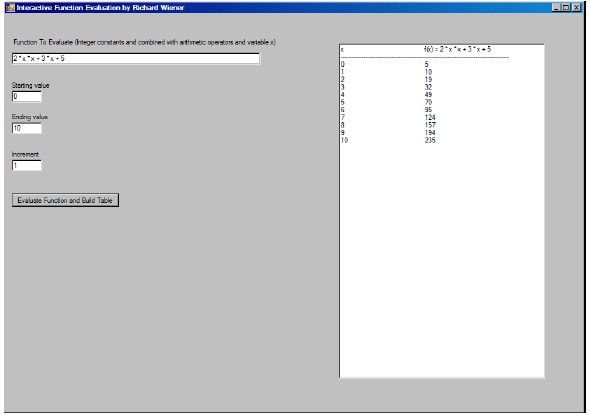
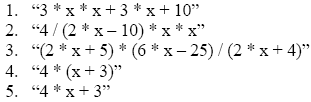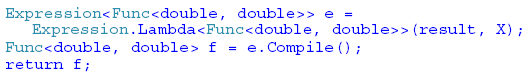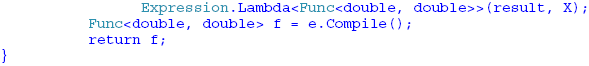1 INTRODUCTIONLambda expressions and expression trees are among several important new features in the recently released C# 3.0/.NET 3.5 framework. An example of a lambda expression that defines a function, g(x) = 2 * x * x + 3 * x + 10 is: Here the first generic parameter indicates that the independent variable, x, is of type double and the second generic parameter, of type double, is the return type. In general a lambda expression is written as a parameter list, followed by the => token, followed by an expression or a statement block. Expression trees, another new C# 3.0 feature, allow lambda expressions to be represented as data structures instead of executable code. Expression trees are "efficient in-memory data representations of lambda expressions and make the structure of the expression transparent and explicit" (Microsoft C# 3.0 Specifications -- http://msdn2.microsoft.com/en-us/library/ms364047(vs.80).aspx#cs3spec_topic9 ). An expression tree could be defined as follows: The variable, expr, is data and may be stored or sent to a remote computer. There it may be "compiled" and converted back to an executable function. This can be accomplished as follows: 2 THE PROBLEMA classic problem in data structure theory is the dynamic evaluation of arithmetic functions. Here the user inputs as a string an arithmetic expression containing constants, parenthesees, one independent variable, say x, and combines these using the operators ‘+', ‘-‘, ‘*' and ‘/'. Some examples of such arithmetic functions would be: Since these functions are input as the program is running the challenge is to be able to dynamically convert each string representation of a function to an internal structure that permits the function to be evaluated for arbitrary values of the independent variable x. In other words we wish to be able to implement dynamic function evaluation. 3 CLASSIC SOLUTIONA classic approach to performing dynamic function evaluation is to first convert the arithmetic expression from its original infix format to postfix. In postfix format, there are no parenthese. Combinations of operands are followed by the appropriate operator. Consider as examples functions 4 and 5 given above. The expression 4 * (x + 3) may be expressed as 4x3+* in postfix format. Reading from right to left, the operands x and 3 are combined using ‘+' and the sum combined with the operand 4 using ‘*'. The expression 4 * x + 3 may be expressed as 4x*3+ in postfix format. Here the operands 4 and x are combined using ‘*' and the result combined with the operand 3 using ‘+'. Once the postfix expression is obtained, a relatively simple algorithm may be used to evaluate the postfix expression. The symbols in the postfix expression are read from left to right. If an operand symbol is read its value (or symbol if it is the independent variable x) is pushed onto a stack. If an operator symbol is read, the stack is popped twice and the two values returned are operated on by the operator symbol and the result pushed back onto the stack. After all the symbols in the postfix string have been read the stack is popped one final time to return the result to the user. It should be simple to see this algorithm in action for the two postfix strings given above. Consider the postfix string 4x*3+. The first two symbols are operands and are pushed onto the stack. The third symbol is an operator so the first two operands are popped from the stack and combined using the ‘*' operator producting 4 * x. This value is pushed back onto the stack. Then the next operand, 3, is pushed onto the stack. Finally, the operator ‘+' causes the two values 4 * x and 3 to be popped and combined with the operator ‘+' producing the value 4 * x + 3 which is pushed onto the stack. Since there are no further symbols, this final value is popped and returned to the user. Further discussion and implementation details in C# may be found in the book Modern Software Development Using C#/.NET by Richard Wiener, published by Thompson in 2007. See pages 604 – 613 for complete details. 4 SOLUTION USING LAMBDA EXPRESSION TREESHere it is assumed that the method InfixToPostfix() returns the postfix format for the input function in the postfix field of the class. Using various static methods from the new C# 3.0 class Expression, an expression tree, result, is obtained. The mechanism follows the algorithm for the evaluation of a postfix expression discussed above. The expression tree, result, is converted to the executable code that the user can use to dynamically evaluate the input function as follows: Here the result of non-generic type Expression is converted to a generic Expression with parameterized type Func<double, double> using the static method Lambda as shown above. Once obtained, it is converted to executable code using the Compile() method. The complete details are given below in Listing 1. Listing 1 – Class FunctionEvaluate A GUI application is constructed that allows the user to input any legal arithmetic expression as well as a starting value, ending value and increment. It then outputs a table displaying the values of the function over the range specified and using the increment provided. A screen shot of this application for the function 2 * x * x + 3 * x + 5 from 0 to 10 with increment of 1 is:'
The code that implements this application is given in Listing 2. This includes the implementation details of converting from infix to postfix. There is no error protection in this code to protect the application from no user input or incorrect user input. It would be relatively easy to add such protection. Listing 2 – Code for Dynamic Function Evaluation Application About the author
Cite this column as follows: Richard Wiener: "Arithmetic Function Interpreter in C# 3.0 Using Lambda Expression Trees", vol. 7, no. 3, March - April 2008, pp 41-48 http://www.jot.fm/issues/issue_2008_03/column4/ |
|||||||