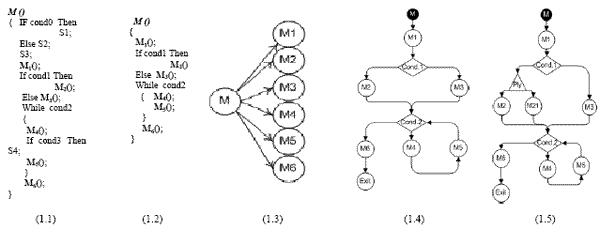
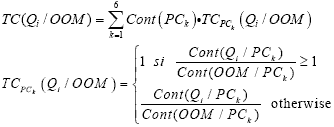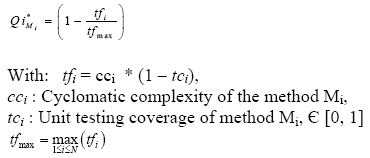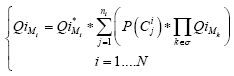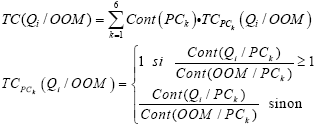AbstractA large number of object-oriented metrics have been proposed in literature. They are used to assess different software attributes. However, it is not obvious for a developer or a project manager to select the metrics that are more useful. Furthermore, these metrics are not completely independent. Using several metrics at the same time is time consuming and can generate a quite large data set, which may be difficult to analyze and interpret. We present, in this paper, a new metric capturing in a unified way several aspects of object-oriented systems quality. The metric uses control flow paths and probabilities, and captures the collaboration between classes. Our objective is not to evaluate a given design by giving absolute values, but more relative values that may be used, for example, to identify in a relative way high-risk classes. We have designed and conducted an empirical study using several large Java projects. We compared the new metric, using the Principal Components Analysis method, to several well known object-oriented metrics. The selected metrics were grouped in five categories: coupling, cohesion, inheritance, complexity and size. The obtained results demonstrate that the proposed metric captures, in a large part, the information provided by the other metrics. 1 INTRODUCTIONSoftware metrics have become a key element in several domains of Software Engineering [Pressman 05, Sommerville 04]. They are used to assess different attributes related to the software product or the process. When applied to software, they allow collecting quantitative data on various aspects related to its attributes. These data are analyzed, eventually compared to historical data when available, and used to improve its quality. The true value of software metrics comes from their association with important external software attributes such as testability, reliability and maintainability [El Emam 01]. Metrics are then used to predict software quality [Fenton 96]. A large number of object-oriented metrics (OOM) have been proposed in literature [Henderson-Sellers 96]. They are used to assess different software attributes such as size, complexity, coupling and cohesion. However, there is a little understanding of the empirical hypotheses and application of many of these metrics [Aggarwal 06]. Moreover, it is not obvious for a developer, a project manager or quality assurance personnel to select the metrics that are more useful. Also, these metrics are not completely independent [Aggarwal 06]. Many of these metrics provide overlapping information. Using several metrics at the same time, particularly in the case of complex and large-scale software systems, is time consuming and can generate a quite large data set, which may be difficult to analyze and interpret. It is then difficult to draw inferences from provided information. We then must limit the number of metrics to be used to a subset of relevant metrics providing useful information. In this paper, we present a new metric, called Quality Indicator (Qi), for assessing classes in object-oriented systems (OOS). The metric has no ambition to capture all aspects related to software quality. The objective is basically to capture, in a unified way, some aspects related to object-oriented systems testability and maintainability. This will allow avoiding using several metrics at the same time. The metric we propose captures, in fact, much more than the simple static structure of a system. We expect that it can be used in place of several existing object-oriented metrics. Our aim, in a first step, is to find in which proportions the Qi metric captures the information provided by some well-known OOM. The measures obtained using our metric are considered, in fact, in a relative way. Our objective is not to assess a given design by providing absolute values, but more relative values which can be used, for example, for: (1) identifying the high-risk classes (in a relative way) that will require a relatively higher testing effort to insure software quality, (2) identifying the fault prone classes, or (3) quantifying the impact of a change instantiated on a given class on the rest of the classes of the system. Testability and maintainability are particularly important software quality attributes as it has been recognized that software testing and maintenance activities are costly phases of software life cycle. With the growing complexity and size of OOS, the ability to reason about such major issues based on automatically computable metrics capturing various aspects related to software quality has become important. The metric we propose is, in fact, multi-dimensional. It captures (indirectly) various aspects related to different internal software attributes, such as complexity and coupling (interactions between classes). It is basically based on control flow paths and probabilities. Size, complexity and coupling are among the most frequently used metrics in practice. There exists empirical evidence for correlating size, complexity and coupling with various quality attributes such as fault-proneness, testability and maintainability. Our objective is, among others, to provide developers and project managers with a metric unifying several existing OOM. The metric we propose has been implemented for Java programs. We have designed and conducted a large empirical study using several Java systems. The analyzed systems vary in size, structure and domain of application. We compared the new metric, using the Principal Components Analysis (PCA) method, to some well known OOM. The selected metrics were grouped in five categories: coupling, cohesion, inheritance, complexity and size. The obtained results show that the proposed metric captures, in a large part, the information provided by the other metrics. As mentionned previously, our objective, in a first step, was to correlate our metric to some well known OOM, validated as quality predictors, and to find in which proportions the Qi metric captures the same underlying properties that these metrics capture. By showing this correlation, we can expect that the new metric can also be used as a quality predictor with the advantage of providing, in a unified way, information about different software attributes. Our aim in this project, as a next step, is to validate the metric as a good predictor of some external software quality attributes such as testability and maintainability and use it to support various tasks related to testing and maintenance activities. The results already obtained from the first experiments we realized in this way, by correlating directly the new metric to some aspects related to testability and changeability of OOS, are very encouraging. These issues will be addressed in a futur paper. The remainder of the paper is organized as follows: Section 2 gives a brief definition of the OOM we selected in this study. The proposed metric is presented in Section 3. Section 4 presents the empirical study we conducted and discusses the obtained results. Finally, Section 5 gives general conclusions and some future work directions. 2 SELECTED OBJECT-ORIENTED METRICSWe give, in this section, a brief definition of the OOM we selected for the empirical study. The selected metrics are: CBO, MIC, MPC, LCOM, TCC, DIT, RFC, WMPC, LOC, NOO. These metrics are used to assess various OOS attributes. We focus, in this paper, on the comparison of our metric, in terms of provided information, to the selected metrics. Coupling MetricsCBO (Coupling Between Objects): CBO counts for a class the number of other classes to which it is coupled [Chidamber 94]. Two classes are coupled when methods declared in one class use methods or instance variables defined by the other class. MIC (Method Invocation Coupling): MIC indicates the relative number of classes to which a given class sends messages. An excessive coupling between classes of a system affects its modularity [Briand 99]. To improve modularity and promote encapsulation, coupling between classes must be reduced [Larman 03]. Well known practices in software engineering tend, in fact, to promote low coupling between classes in OOS to facilitate evolution [Larman 03, Sommerville 04, Pressman 05]. Furthermore, the more the coupling is high, the more the system is affected by changes (ripple-effect) and the more its maintenance is difficult. The comprehension of a highly coupled class is difficult since it implies the comprehension of the classes it is coupled to. Aggarwal et al. [Aggarwal 06] addressed recently the correlation between some existing coupling metrics and their relationship to fault proneness. The defined prediction model shows that coupling metrics are highly correlated to fault proneness. The measure of coupling is also a good indicator of testability. Cohesion MetricsLCOM (Lack of COhesion in Methods): LCOM measures the dissimilarity of methods in a class [Chidamber 94]. It is defined as follows: Let P be the number of pairs of methods that do not share a common attribute and Q the number of pairs of methods sharing a common attribute, LCOM = |P| - |Q|, if |P| > |Q|. If the difference is negative, LCOM is set to 0. TCC (Tight Class Cohesion): TCC gives the relative number of pairs of methods directly connected [Bieman 95]. Two methods are connected if they access a common instance variable of the class. In a class C, if the number of methods is equal to n, then NP(c) the number of pairs of methods is given by: n (n-1) /2. Let ND(C) be the number of pairs of methods of the class that access directly the same instance variable. TCC is then given by: NP(C) / ND(C). Class cohesion is considered as one of most important attributes of OOS. Cohesion refers to the degree of relatedness between members in a class. A high cohesion in a class is a desirable property [Larman 03]. It is widely recognized that highly cohesive components tend to have high maintainability and reusability [Li 93, Bieman 95, Basili 96, Briand 97, Chae 00]. The cohesion of a component allows the measurement of its structure quality. The cohesion degree of a component is high, if it implements a single logical function. Inheritance MetricsDIT (Depth of Inheritance Tree): DIT of a class is given by the length of the inheritance path from the root of the inheritance hierarchy to the class on which it is measured (number of ancestor classes) [Chidamber 94]. Inheritance allows a better reusability of the code. Complexity MetricsRFC (Response for a Class): The response set of a class is defined as the set of methods that can be potentially executed in response to a message received by an object of that class [Chidamber 94]. A class with a high response set is considered more complex and requires more testing effort. WMPC (Weighted Methods Per Class): It represents the sum of the complexities (normalized cyclomatic complexity) of all the methods of a given class [Chidamber 94]. Only the specified methods in the class are considered. The number of methods and their complexity are indicators of the effort required to develop, to test and to maintain the class. Cyclomatic complexity has been validated as a good indicator of fault proneness. A high complexity is synonym of a higher risk of faults in the class, also a more difficult comprehension [Basili 96, El Emam 01]. Size Metrics LOC (Lines Of Code): LOC counts the number of lines of code. A large class is difficult to reuse, to understand and to maintain, and it presents a higher risk of faults [El Emam 01]. Size is a significant predictor of maintainability [Dagpinar 03]. 3 QUALITY INDICATORThe metric we propose, called Quality Indicator (Qi) of classes, is based on control call graphs, a reduced form of control flow graphs. It takes into account the interactions between classes (collaboration between classes) and their related control. It also integrates the probability of call of the methods depending on the control flow in a program. The Qi metric is normalized and gives values between 0 and 1. The Qi metric is, in fact, a refinement of the basic metric used by Badri et al. in [Badri 95] to support OOS integration testing. Control Call GraphsA Control Call Graph (CCG) is a reduced form of a Control Flow Graph (CFG). The nodes representing instructions not leading to method calls are removed. Let us consider the example of the method M given in figure 1.1. S1 represents sequences of instructions that do not contain method calls. The code of method M reduced to control call flow is given in figure 1.2. The corresponding call graph is given in figure 1.3. Figure 1.4 gives the control call graph of method M. Contrary to traditional call graphs (CG), CCG better summarize the control and model the control flow paths that include interactions between methods. They better capture the structure of calls. Polymorphism and CCGPolymorphism is difficult to capture by a simple static analysis of the source code. In fact, the effective call of a virtual method is done when executing the code (dynamic binding). In our approach, polymorphic messages that figure in the CCG of a method are marked. A node corresponding to a polymorphic call is represented by a polygon of n+1 sides, n being the number of methods that can eventually respond to the call. The vertices of the polygon are linked by directed arcs to the virtual methods that can eventually respond to the call. The list of methods that can potentially respond to the call is determined by static analysis of the code. If we consider, from the example given in figure 1, that call M2 is polymorphic and that a method M21 can also respond to the call, the extension of the CCG of method M, while taking into consideration polymorphism, is given by figure 1.5.
Figure 1: A method and corresponding CG, CCG and polymorphic CCG. Generating the Qi metricsGenerating the Qi metrics is done in three major stages: Stage 1: Extracting, by static analysis of the source code of the program, the CCG of each method. Stage 2: Transforming the CCG of each method in a model that will allow the evaluation of its Qi. The Qi of a method is expressed, in fact, in terms of several intrinsic parameters of the method such as its unit testing coverage and its cyclomatic complexity, as well as the Qi of all the methods it calls. We start from the principle that the quality of a method, in particular in terms of reliability, depends also on the quality of the methods with which it collaborates to accomplish its task. In OOS, the objects collaborate to achieve their respective responsibilities. A method of low quality, presenting for example faults, or a low testing coverage, can have an impact on the methods that use it (directly or indirectly) depending on the control flow. In other words, its low quality can affect the quality of other methods collaborating with it. There exists here a propagation that needs to be captured (interference between classes). For example, if we consider two classes with (let us suppose) the same complexity but used in two different ways. The first one may be used lowly and the second one used highly in the system. The impact of a poor quality of the second one risk being more important than the first one. It is not obvious, particularly in the case of complex and large software systems, to identify intuitively this type of interference between classes. This kind of information is not captured by the selected OOM. The Qi of each method is expressed under the form of an equation. The details relative to this step will be presented in what follows. As mentioned previously, the obtained values are mainly considered in a relative way. They allow determining, among other things, the most critical parts (in a relative way) of a program. The Qi of each class is calculated in function of the Qi of its methods. We obtain a system of n equations (n being the number of methods in the program). Stage 3: Finding a solution to the system of equations to obtain the values of the Qi of the classes (by going through the ones of the methods) of the system. Assigning ProbabilitiesThe CCG of a method can be seen as a set of paths that the control flow can cross. Taking a path depends on the conditions in the control structures. To capture this probabilistic characteristic of the control flow, we assign a probability to each path defined in the CCG as follows: For a path Ck, where Ai are the directed arcs composing the path Ck. By supposing, to simplify the analysis and the calculations, that the conditions in the loop structures are independent, the P(Ai) becomes the probability of an arc of being taken when exiting a control structure. The P(Ck) are then reduced to a product of the probabilities of the state of the conditions in the control structures. To simplify our experiments, we assigned probabilities to the different control structures according to the rules given in Table 1. These values are assigned automatically during the static analysis of the source code when generating the different Qi models. This is done by a tool we developed. As an alternative way, the probability values would also be obtained by dynamic analysis (according to the operational profile of the program), or assigned by programmers from the knowledge of the program. Dynamic analysis will be considered in a future work.
Table 1: Assignment rules of the probabilities. Quality IndicatorFor a method Mi, we define its Qi as a kind of estimation of the probability that the control flow will go through the method without any “failure”. The Qi of a method, such as mentioned previously, is calculated in function of the Qi of the methods it calls, of the probability of those methods to be called, and of an intrinsic constant of method Mi called Intrinsic Quality Indicator (or Intrinsic Qi) of the method. The intrinsic Qi of a method regroups basically some parameters related to its testability. The Qi of a method Mi is given by: Intrinsic Quality IndicatorThe Intrinsic Quality Indicator of a method Mi, noted Qi*aMi, regroups some parameters characterising in an intrinsic way the method. These parameters are related to the cyclomatic complexity and testing effort of the method. It informs somewhere on the quality (in terms of level of confidence that we can have towards the method) that this method would have if all the methods it calls have a high quality (completely tested for example). It allows informing on the confidence that we can give to the method and also on the risk that its execution may present (on the system or on some parts of the system). In other words, we can have a high level of confidence towards a method having a high complexity but tested completely. Towards the same method, if for example it has been tested partlialy (testing coverage of 25 %), will have a relative low level of confidence. As mentioned previously, the measures obtained using the Qi metric are basically considered in a relative way. One of our main objectives is to determine, for example, the high-risk parts of a program on which a supplementary testing effort (relative to the other elements) should be relevant. The dependencies between methods (and at a high level between classes) play an important role in this context. In fact, if we consider for example two methods M1 and M2 of low quality (with comparable complexities and testing coverages), and M1 strongly used in the system relatively to M2, M1 will probably have an impact more likely important than M2. Classes in OOS collaborate to accomplish their tasks. These classes have in general different complexities, as well as different roles in the system, depending on their intrinsic characteristics and responsibilities. Some classes are more “important” than others (key classes). Instantiating changes on these classes, for example, can have more consequences (impact sets and reliability particularly) on the system (or parts of the system) than another classes. The Intrinsic Quality Indicator of a method Mi includes its cyclomatic complexity as well as its unit testing coverage and is defined as: Complexity can help software engineers determining a program’s inherent risk. In fact, cyclomatic complexity is a good indicator of fault proneness. Studies show a correlation between a program’s cyclomatic complexity and its error frequency. A low cyclomatic complexity contributes to a program’s understandability. Cyclomatic complexity is also recognized as a strong indicator of testability. The more the cyclomatic complexity of a method is high, the more likely its testing effort would be high. We assume in our approach that a testing coverage of 1 corresponds to a completely tested method. A testing coverage of 0 corresponds to a method not tested at all. The Quality Indicator of a method that does not call any other method is reduced to its Intrinsic Quality Indicator. A method that does not call any other method, and that was completely tested for example, would have a Quality Indicator value of 1. System of equations: ResolutionBy applying the previous formula to each method, we obtain the following system of equations:
The obtained system of equations is not linear. Its size is equal to the number of the methods of the program. It is composed of several multivariate polynomials. We use an iterative method to solve it (method of successive approximations). The system is reduced to a fixed point problem. For reasons of space limitation, we do not give the details corresponding to the demonstration of the existence of the solution. We compute the n iterations to be done to obtain an error in the order of 10-5. We define the Qi of a class as the product of the Qi of its public methods. The calculation of the Qi is entirely automated by an Eclipse plug-in tool that we developed in Java. We also use the scientific calculation software Scilab. 4 EMPIRICAL STUDYWe present, in this section, the empirical study we conducted to evaluate the Qi metric and the selected OOM. We describe in what follows the methodology used to collect and analyze the metrics data for the selected systems. The experiments, performed on several Java projects, had essentially for objective (in the context of this paper) to evaluate the capacity of the Qi metric to capture the information provided by the other metrics. Methodology and Data Collection The selected OOM have been computed using the Together tool (Borland). The Qi have been computed using the Eclipse plug-in tool we developed. For our experiments, we fixed the unit testing coverage to 75% for each of the methods of the analyzed systems. Furthermore, we evaluated other values of testing coverage. The obtained results where substantially the same (in a relative way). The statistical computations were done using the 2007 XLSTAT tool. The methodology followed for the first series of the experiments we performed in this project is based on a Principal Components Analysis (PCA). The analysis is done on the entire data set of the considered metrics, including the Qi values. We evaluated the percentage of capture of the information provided by the OOM by the Qi. We selected seven open source Java projects from various domains:
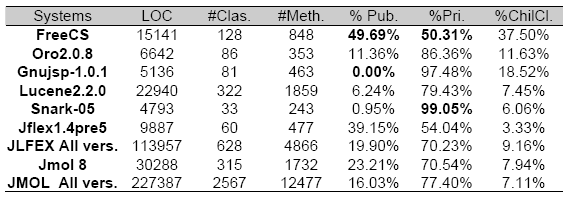
Descriptive StatisticsTable 2 gives some descriptive statistics on the analyzed systems. The 29 analyzed programs totaled approximately 400 000 lines of code, 4000 classes and 21 600 methods. For the systems selected in several versions (JFlex, JMol), only the last version is given in Table 2. Inheritance is also present in the set of selected systems. In fact, 8.7 % of classes inherit from a basic class other than Java Object class. This will allow us to evaluate the Qi metric in presence of inheritance. Furthermore, the number of public and private variables in the analyzed systems indicates the encapsulation of data. We also wanted to evaluate how the Qi behave regarding this aspect. Table 3 gives descriptive statistics (minimum, maximum, mean value) on the selected metrics.
Table 2: Descriptive statistics of the analyzed systems.
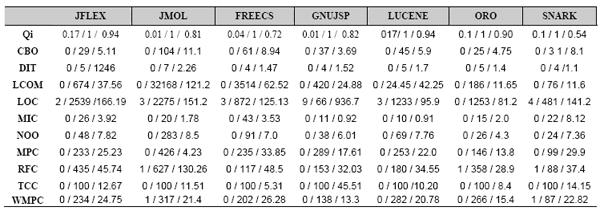
Table 3: Descriptive statistics on the selected metrics. Principal Components AnalysisPrincipal Component Analysis (PCA) is a standard technique to identify the underlying orthogonal dimensions that explain relations between variables (our metrics here) in a data set. Principal Components (PCs) are linear combinations of the standardized independent variables. PCA is one of the most used multivariate data analysis method. There exist several applications of PCA. We focus in this paper on the study and visualization of correlations between variables. PCA is based on a projection principle. It projects the observations from a space at p dimensions of the p variables to a space at k dimensions (k < p) such that a maximum of information is kept on the first dimensions. The information is measured here through the total variance or a cloud of points. If the information associated to the first 2 or 3 axes represents a sufficient percentage of the total variance of the cloud of points, we then can represent the observations on a graph with 2 or 3 dimensions. This simplifies the interpretation. This is an important element of software measurement, since it allows determining the basic elements that provide most information. PCA uses a matrix that indicates the degree of similarity between variables to calculate the matrices that will allow projecting the variable into a new space. It is common to use as a similitude indicator the Pearson correlation. When the PCA stage will be completed, our approach will consist on computing the global contribution of each metric on the first components representing 95% of provided information. We will compute the percentage of capture of the information provided by each metric by Qi. This will allow us to see to what degree Qi can be used to replace certain metrics.
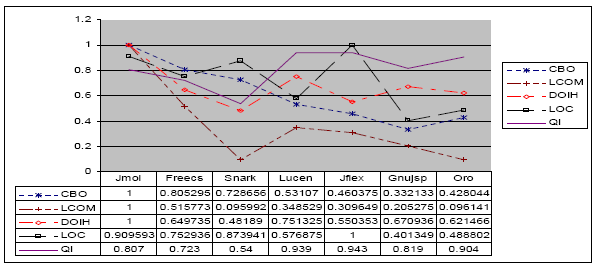
Figure 2: Tendencies of the major metrics. Figure 2 shows the tendencies of some of the selected OOM, as well as the Qi. Following are the observations made from the first results:
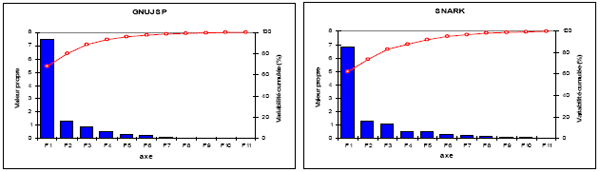
Data Analysis and ResultsThe values in bold in the following tables (4 – 10) are significantly different from 0 (with alpha = 0.05) for all correlation matrices. The negative signs of the correlations detain all their respective meaning. According to the definition of Qi, as quality indicators, we expect that a high value of Qi (near 1) is a sign of good design (in a relative way) for a class. The correlation signs all show that Qi decreases, with: (1) The increase of coupling (CBO, MIC); (2) The decrease of cohesion (increasing LCOM and decreasing of TCC); (3) The increase of the depth of inheritance (when it is significant, JMOL has the highest level of inheritance of all the analyzed projects with 2.264); (4) The increase of cyclomatic complexity (WMPC, RFC); and (5) The increase of size (increase of LOC, NOO, RFC). JFLEX (Table 4) shows significant correlations between Qi and all the other metrics, except the DIT metric. The low sensitivity of Qi against DIT can be explained by a weak usage of inheritance in JFLEX (the second lowest value after SNARK). This seems indicating that a moderated usage of inheritance does not affect Qi. Qi and LOC are highly correlated. The negative sign of this correlation shows that the increase in lines of code (size) degrades the value of Qi, which confirms our hypotheses. We then can see that a high and significant correlation between Qi and LCOM is observed for all systems. In our model, Qi do not take into consideration explicitly the data flow. From that fact, we can think that there is no link between cohesion (in the LCOM sense) and Qi. However, Qi captures the interactions between methods, which could partially explain this correlation. JMOL (table 5) is a graphical application where the design is highly based on inheritance. The descriptive statistics indicate that it is the system that contains the most depth inheritance structures (2.264 in average) among the analyzed systems. The effect of this structure on the decreasing value of Qi is denoted by the appearance of a significant correlation of -0.34. The negative sign implies a degradation of Qi with the increasing of DIT. In the case of FREECS (table 6), the non significant correlation between Qi and DIT seems confirming that the low usage of inheritance (0.65) has no incidence on Qi. GNUJSP (table 7) presents significant correlations between Qi and the other metrics, except for DIT. Once again, the inheritance structure of GNUJSP seems reasonable when looking at the descriptive statistics given earlier. The other systems present similar results as for GNUJSP. However, we can note that for these systems, the correlation between Qi and TCC is not significant. This seems, however, indicating that TCC and LCOM do not capture the same dimension of cohesion in certain cases. This aspect was also mentioned in some papers addressing cohesion in OOS. For the correlation matrices of GNUJSP, ORO, LUCENE, FREECS and SNARK, the observations made regarding JFLEX and JMOL are confirmed, meaning that of the correlations with DIT, always non significant, are explained by the use of a little deep hierarchy in these programs. Furthermore, we can note the following: (1) The correlation between TCC and Qi is significant and high for GNUJSP. (2) The correlation between RFC and TCC is difficult to interpret since it is significant in certain projects and of changing signs: 0.24 for ORO and -0.58 for JSP. (3) The high correlation that exists between DIT and RFC makes the RFC metric difficult for interpretation. In fact, this metric is too sensitive to DIT. Since a high value and a too low value of DIT are not desirable, RFC becomes difficult to interpret, since it must be minimized for a better testability. Variability of the PCsTo have at least 95% of the information captured by the metrics, which is largely sufficient, we will retain the first 6 principal components. We give in what follows the observed variability for two systems (figures 3 and 4). The distribution of information on the first components is uniform enough for the different projects. However, it is more concentrated on the first components for GNUJSP. In what follows, the other components will be ignored.
Figure 3: Variability for GNUJSP Figure 4: Variability for SNARK While performing a PCA on the same data set, but without Qi, we can observe a decrease in the variability of the first components. This seems indicating that Quality Indicators capture the information provided by several metrics, but they also bring in more information. This has for effect to better center the information on the first component. Table 11 shows the percentage of the informational data of the first principal component (PC1) before and after the integration of the Quality Indicators in the analysis.
Table 11: Variability of the first component without and with the values of Qi.
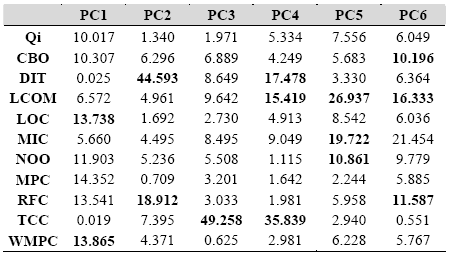
Table 12: Mean contributions of the metrics on the PCs. Contribution of the metricsPCA gives the contribution of each metric on the obtained components. While interested in the first components and considering what was mentioned previously (95% of the total information), we can list the set of metrics captured by the Qi and quantify in terms of percentage their capture by Qi on the level of each principal component (PC) and on a global level while considering the first principal components together. Table 12 shows the quantity of information (mean value for the selected systems) provided by each metric on the PCs. We can calculate, for each PC, the quantity of information that the Quality Indicators Qi provide and that the other metrics provide. Inspired from the work of Aggarwal et al. [Aggarwal 06], we can associate each PC to a quality attribute.
Coverage of the selected metricsIn this section, we illustrate how we compute the coverage ratio of the selected OOM metrics by the Quality Indicators Qi. With: Cont(PCk) being the percentage of the contribution of component PCk on the entire data set, Cont(Qi/PCk) the percentage of the contribution of the Quality Indicator Qi in component PCk, and Cont(OOM/PCk) the percentage of contribution of the OOM metric in component PCk. Table 13 gives the obtained results for each project as well as the average for all projects.
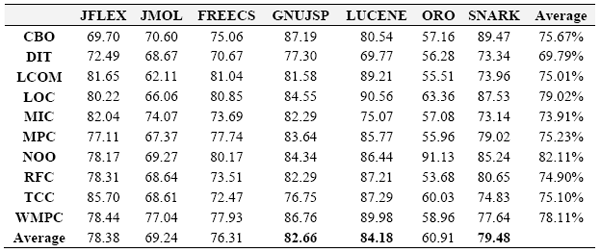
Table 13: Coverage of the selected metrics by the Qi. For CBO: according to the obtained results, this coupling metric can be replaced by Qi, since Qi captures up to 75.67% of the information it provides. This is explained by the consideration (in an implicit manner, according to the formulation of the Qi model) of the effective coupling through method calls by the Qi model. The remainder of the not captured information is found into the following: (1) Coupling due to data flow, coupling that Qi do not capture. Note that GNUJSP and SNARK have the highest capture levels of CBO by Qi. In fact, GNUJSP and SNARK have few public variables (0% for GNUJSP and 1% for SNARK). Therefore, all flow exchanges between classes (effective coupling) are done through method calls. (2) Coupling with system libraries, which are also ignored by Qi. For DIT: This metric is partially captured (69.8%) by Qi. However, we mentioned previously that Qi becomes sensitive to DIT solely when the inheritance is very present in the project. The obtained results seems indicating that Qi can be used instead of DIT to detect the effects of a very complex inheritance mechanism in a project. LCOM: Qi not having a direct relation to cohesion in the sense of LCOM, the good coverage of Qi observed for this metric (75.01%) can be explained by the interactions between methods that Qi captures, and also possibly by the indirect use of a coupling metric. By admitting also that a low cohesion leads to a high coupling, this decreases Qi. The (negative) relationship that exists between coupling and cohesion was the subject of a recent paper of Badri & al. [Badri 08]. LOC: The size of a system varies in the same way that complexity does, and certain of other metrics; this can explain the 79.02% coverage by Qi. WMPC represents the cyclomatic complexity. It is present in the Quality Indicator model through the Intrinsic Quality Indicator of the methods, which explains a capture ratio of 78.11%. The remaining information on complexity is composed of the arcs of the graph that do not lead to method calls, therefore ignored by our model. We observe that the higher coverage values of Qi are for the projects Gnujsp, Snark and Lucene, with respectively 82.6, 79.48 and 84.1. This seems to be related to the fact that in these projects the percentage of public variables is low. This means that in the case of these projects the control flow is much more important than the data flow. 5 CONCLUSIONSWe presented, in this paper, a new model that can be used to assess several attributes of OOS. The model, called Quality Indicator, uses control flow paths and probabilities, and captures the collaboration between classes. We conducted an empirical study using several Java projects. The collected data set was enough large. We compared the new model, using the Principal Components Analysis method, to several well known OOM. The metrics where grouped in five categories (coupling, cohesion, inheritance, complexity and size). The obtained results show that the proposed model captures more than 75% of the information provided by the selected metrics (CBO, MIC, LCOM, TCC, DIT, RFC, WMPC, LOC and NOM). For some metrics, the capture is done directly. In fact, WMPC, NOM and CBO are indirectly included in the Qi model. Furthermore, the Qi capture DIT only if the inheritance is significant in the analyzed system. We noted also that the encapsulation of data is very important to give sense to the results provided by the Qi model. Encapsulation of data is a desirable property of object-oriented systems. We believe that the model captures much more than the simple static structure of a system. It presents the advantage, compared to other OOM, of unifying various aspects related to OOS attributes. We plan to replicate our study on other large projects to be able to give generalized results. We also plan to evaluate the Qi model as predictor of testability, fault proneness and maintainability. The results already obtained from the first experiments we realized in this way are very encouraging. Our aim is to use the model for supporting various activities related to testing and maintenance of OOS. ACKNOWLEDGEMENTSThis work was supported by a NSERC (Natural Sciences and Engineering Research Council of Canada) grant. REFERENCES[Aggarwal 06] K.K. Aggarwal, Y. Singh, A. Kaur and R. Malhotra: “Empirical study of object-oriented metrics”, In Journal of Object Technology, vol. 5, no. 8, November-December 2006. [Badri 95] M. Badri, L. Badri and S. Layachi: “Vers une stratégie de tests unitaires et d’intégration des classes dans les systèmes orientés objet” , Revue Génie Logiciel, no. 38, Décembre 1995. [Badri 08] L. Badri, M. Badri and A.B. Gueye: “Revisiting class cohesion: An Empirical Investigation on Several Systems”, In Journal of Object technology, vol. 7, no. 6, July-August 2008. [Basili 96] V.R. Basili, L.C. Briand, and W.L. Melo: “A Validation of Object-Oriented Design Metrics as Quality Indicators”, IEEE Transactions on Software Engineering, vol. 22, no. 10, pp. 751-761, October 1996. [Bieman 95] J.M. Bieman, B.K. Kang: “Cohesion and Reuse in an Object-Oriented System”, Proceedings of the ACM Symposium on Software Reusability, April 1995. [Briand 97] L.C. Briand, J. Daly and J. Wurs: “The dimensions of coupling in object-oriented systems”, Proceedings of OOPSLA, 1997. [Briand 99] L.C. Briand, J. Wüst, and H. Lounis: “Using Coupling Measuremen tfor Impact Analysis in Object-Oriented Systems”, Proc. of the IEEE International Conference on Software Maintenance (ICSM), pp. 475-482, Aug./Sept. 1999. [Chae 00] H.S. Chae, Y.R. Know and D.H. Bae: “A cohesion measure for object-oriented classes”, Software Ptractice and Experience, no. 30, 2000. [Chidamber 94] S.R. Chidamber, C.F. Kemerer: “A metrics Suite for Object Oriented Design”, IEEE Transactions on Software Engineering, Vol.20, No.6, June 1994. [Dagpinar 03] M. Dagpinar and J.H. Jahnke: “Predicting Maintainability with Object-Oriented Metrics – An Empirical Comparison”, Proceedings of the 10th Working Conference on Reverse Engineering, 2003. [El Emam 01] El Emam, K.; Benlarbi, S.; Goel, N. and Rai, S. N.: “ The confounding effect of class size on the validity of object-oriented metrics”, IEEE Transactions on Software Engineering, 27(7): 630-650, 2001. [Fenton 96] N. Fenton et al.: Software Metrics : “A Rigorous and Practical Approach”, International Thomson Computer Press, 1996. [Henderson-Sellers 96] B. Henderson-Sellers: “Object-Oriented Metrics, Measures of Complexity”, Prentice Hall, 1996. [Larman 03] G. Larman: Applying UML and Design Patterns, An introduction to object-oriented analysis and design and the unified process, second edition, Prentice-Hall, 2003. [Li 93] W. Li and S. Henry: “Object-Oriented metrics that predict Maintainability”, Journal of Systems and Software, vol. 23, 1993. [Pressman 05] R.S. Pressman: Software Engineering, A practitionner’s approach, sixth edition, Mc Graw Hill, 2005. [Somerville 04] I. Sommerville: Software Engineering, 7th edition, Addison Wesley, 2004. About the authors
|
|||||||||||||