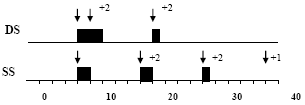
AbstractObject-oriented programming languages are being widely adopted as one of the most powerful languages due their flexibility and reusability. However, these languages suffer from memory mismanagement that could be critical especially in real-time and embedded systems. Automatic memory management through garbage collector handles this problem. Concurrent garbage collection based on sporadic or deferrable server is considered the most famous collectors in this area. In such algorithms, the garbage collection task is assumed to be the single aperiodic task in the system. When there are other different types of traffic, with short deadlines and long deadlines, the single server provides poor performance. The garbage collection task may have to wait till a less urgent or a higher deadline request finishes its execution that leads to an increase in the system memory requirement and perhaps a deadline miss of the garbage collection thread. This paper concentrates on minimizing the system memory requirement when there are multiple sources of events by introducing a new concurrent garbage collector. In the proposed collector, the system will have multiple servers; rather than one as in the available garbage collectors. These servers can either share or not share their capacities, i.e. a server can use the unused capacity of other servers in case of sharing. The two schemes give preference to higher priority servers. We also propose a modification in the copying collector that enhances its performance. The simulation results show that using multiple servers with capacity sharing in garbage collection scheduling strategy exhibits a better performance in terms of reducing the system memory requirement and meeting most of deadlines than using either single server or multiple servers without capacity sharing collectors. However, the capacity-sharing scheme gave lower response times for jobs with short deadlines, like GC task, than without capacity sharing scheme. 1 INTRODUCTIONMemory management in real-time and embedded systems is handled using automatic memory management (i.e. Garbage Collection or GC for short) which enables the programmers to overcome the potential danger of manual memory management, such as memory leaks, dangling pointers, fragmentation, and so on. The garbage collector distinguishes the memory objects that are no longer in use (garbage) from the live objects and reclaims the garbage for future use [1, 4]. The advent of garbage collection to the real-time scene causes serious obstacles as traditional garbage collection threatens the schedulability and predictability of tasks that demand strict real-time requirement. So, some effort had been put in order to make it suited to real-time systems. Scheduling incremental garbage collection algorithms was the solution to enhance the position of garbage collection in the real-time scene. The main aim towards scheduling garbage collection is to achieve low overhead and enough predictability for hard real-time tasks. Many works in the literature have classified garbage collection scheduling mechanisms into two categories: sequential and concurrent garbage collection [4]. Sequential garbage collection failed to achieve the aims of GC scheduling in real-time systems. Thus, the main trend is towards concurrent GC techniques. Concurrent GC is a great step towards truly and efficient real-time garbage collection algorithms. Some variants of concurrent GC have been developed. Among them are the background approach [4], Metronome [5], time-triggered GC and its auto-tuning form [1, 12]. Although all of these approaches remove the obstacles caused by traditional garbage collection in real-time systems, they rely on a relatively large amount of redundant system memory. So, some other concurrent GC algorithms had been put on reducing the system memory requirement and guaranteeing the schedulability of hard real-time mutators under automatic memory management. Among these techniques are the sporadic server (SS) based GC [3] and the deferrable server (DS) based GC [2]. Both of them are based on the resource reserving mechanism. A garbage collector is treated as a periodic or aperiodic task and is scheduled concurrently with other tasks in the system. The deferrable server based GC achieves the most minimum worst-case response time of a garbage collector among all other concurrent garbage collectors. It also achieves the minimum worst-case system memory requirement while meeting hard deadlines for all tasks [2]. The two latter GC scheduling strategies are single aperiodic server based garbage collector. In such algorithms, the GC task is assumed to be the only aperiodic task overall the system. Although the single server minimizes the number of capacity exhaustions, it provides poor performance when there are several aperiodic jobs with different temporal requirement. A single server processes the jobs in a FIFO (First Input First Output) order that is not a good policy [13]. This can lead to the situation in which a short (and urgent request) is delayed due to the fact that the server is processing a long request. The case in which the GC thread may have to wait till a less urgent or a higher deadline request finishes its execution that leads to an increase in the system memory requirement and perhaps a deadline miss of the GC thread. To alleviate the problem of FIFO, other queuing disciplines were used like the SRO (Shortest Remaining Time at Overrun) [13]. However, the event at the head of the queue is still non-preemptive and the rest of the jobs in the queue have to wait until it finishes which delays the response times of lower deadline threads like the GC task that may have to wait till a higher deadline ones execute. The aforementioned problem can be solved using multiple servers at different priorities [14]. The priority assigned to servers is done at a priority level that commensurates with the deadline of the jobs it serves. This scheme is truly preemptive; if the server that handles the long deadline aperiodic request is running while the urgent or lower deadline request arrives; the processor will be immediately switched to the high priority server. The servers can use the sharing or non-sharing protocol. This paper proposes a new concurrent garbage collector based on multiple servers. There are two possible schemes when using multiple servers; sharing capacity and non-sharing capacity [14]. In capacity sharing scheme, a server can use the unused capacity of other servers, while in non-sharing scheme this sharing is not allowed between the servers. 2 BACKGROUND AND PREVIOUS WORKMany literatures have categorized the garbage collection algorithms into two classes: reference counting and tracing. Reference counting requires an additional reference count (RC) field for each object [5, 15]. Whenever a pointer has been changed by a mutator, RC field is also updated. When the RC value drops to zero, the object is reclaimed immediately. The tracing algorithm is classified again into mark-sweep and copying. The mark-sweep collector traverses the pointers to find live objects and marks them. Then, a collector scans the entire heap and reclaims garbage objects that have not been marked. Typically copying collectors maintain two equal-sized spaces called fromspace and tospace. When a garbage collector is triggered, it traverses the pointers and copies the live objects into the new tospace. The basic tracing garbage collection algorithms are inherently stop-the-world fashion, and sometimes their pause time is intolerable for the applications that require short or bounded response time. Incremental garbage collection algorithms [2, 4, 17] have been proposed to distribute and hide the garbage collection pause time throughout the execution of mutators. This approach, in effect, reduces the intermediate pause delay, but it is difficult to guarantee the schedulability of real-time tasks without cooperation with the scheduling mechanism. The most common strategies of the GC is the concurrent GC. It is based on the resource reserving mechanism. The resource here means both CPU and memory. While CPU is reserved for GC, the memory is reserved for the other tasks. A garbage collector is treated as a periodic or aperiodic task and is scheduled concurrently with other tasks in the system. The diversity of this strategy is presented by [1, 11, 14]. Although the concurrent GC solved the problems of traditional GC in real-time systems, they are not optimized solutions because the amount of the worst-case system memory requirement can be reduced further. One way for reducing the system memory requirement problem is the deferrable server based GC scheduling strategy [26]. It is a concurrent garbage collector that is based on a deferrable server together with a particular parameter configuration scheme. This parameter configuration scheme could also be applied into other approaches such as the sporadic server (SS) based GC and time-based GC. The benefits were to minimize the worst-case response time of a garbage collector, and so is the worst-case system memory requirement, with the schedulability of tasks with hard time constraint not jeopardized. Sporadic Server Based GCKim, et al. designed a concurrent GC based on a sporadic server (SS) [14]. It treats GC as an aperiodic task and utilizes the classic aperiodic server strategy of scheduling aperiodic tasks in real-time systems. Figure 1 shows the behavior servicing an aperiodic task using SS. A sporadic server is used to serve the needs of GC, and the period for the server is equal to that for the highest priority periodic task. Since the priorities are assigned under the rule of Rate Monotonic (RM) scheme, the period for the server is the shortest among all tasks. On the other hand, in order to meet the deadlines of all periodic tasks, the utilization of the sporadic server (given by the portion of the capacity out of one period) must be kept in a limited range. The result is that the capacity is very small and usually not enough for a GC cycle. Thus, a single GC cycle may last several periods of the server before it completes, which increases the worst-case response time of GC and there's a need for a certain amount of available memory during the long GC cycle. However, this algorithm shows better performance on reducing the system memory requirement than the background approach. DS based GCYugiang Xian and Gaungze Xiong designed a concurrent GC based on the deferrable server algorithm [24]. It resembles the sporadic server based GC in treating GC as an aperiodic activity. It assumes that the GC is the only aperiodic task in the system (this is only for simplicity). It utilizes the deferrable server strategy of scheduling aperiodic tasks in real-time systems. Figure 1 shows the behavior servicing an aperiodic task using DS. The server has the shortest period among all other tasks; consequently, it will be assigned the highest priority according to the rate monotonic scheduling strategy. The capacity of the server is selected through a particular parameter configuration scheme. This Scheme is addressed using two different approaches, that is, the utilization based analysis and exact analysis of the selection of parameters. The exact analysis is better than the utilization one in parameter calculation because it takes into consideration the individual task set. In this way, DS based GC achieves the worst case response time for the GC thread compared with all previous concurrent garbage collectors. So, it achieves the best results in minimizing the system memory requirement with the schedulability of tasks with hard time constraint not jeopardized.
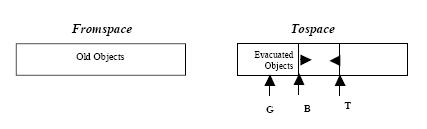
Figure 1. The behaviors servicing an aperiodic task of DD and SS (The arrows with a number accompanying means replenishment) Incremental Copying CollectorThis subsection presents the basic idea of operation for incremental copying collectors [4, 8, 9, 11]. In most copying collectors, the heap is divided into two equally sized areas denoted tospace and fromspace, as illustrated in Figure 2. New objects are allocated at the top of tospace, at the position denoted by T. Allocation proceeds in this way until tospace is filled up. Then, a flip is performed, changing the meaning of tospace and fromspace. The old tospace now becomes fromspace and vice versa. Fromspace will contain a mixture of live and dead objects. The live objects must be moved, evacuated, from fromspace into tospace in order to enable a future flip. The evacuated objects are placed at the bottom, at the location denoted by B. The evacuation procedure is performed incrementally as new objects are allocated at the top of tospace. When no free memory remains in tospace, another flip is performed, effectively reclaiming the memory occupied by dead objects. Another GC cycle is now initiated, evacuating the live objects from the new tospace.
Figure 2. The heap of incremental copying garbage collector B: evacuation pointer, S: scan pointer, T: allocation pointer The notion of tri-color marking terminology [15] is useful when discussing incremental tracing algorithms like the incremental copying collector. Heap objects can be in one of three different states as seen by the garbage collector. These states are denoted black, grey and white. Black objects are those objects that have been marked as being reachable and their contents have been scanned for pointers to other reachable objects. Grey objects are those objects that have been identified as reachable but they have not been scanned for pointers to other live objects. While white objects are those objects that have not been found yet by the garbage collector. Since the mutator executes interleaved with the collector, we must make sure it does not introduce pointers to fromspace objects into black objects. Assignments to pointers are monitored by the write barrier [16] and attempts to violate the consistency of the GC scheme are caught. It was proposed that instead of evacuating the fromspace object immediately, the write-barrier reserves an area for the objects for lazy evacuation [4]. A background garbage collector evacuates the object before the normal evacuation process. However, in the proposed technique, we will use the incremental copying collector mentioned in [3] which adds modifications to the original technique. In the new environment, the garbage collector scans the root-set incrementally while traditional approaches scan the root-set entirely before normal evacuation. There are two kinds of tasks that run on the system: periodic and aperiodic tasks. This paper suggests that the scan and evacuation processes of aperiodic tasks are performed first. This is performed on each task one after another according to the first coming first scanned and evacuated principle. Afterwards, the scan and evacuation of periodic tasks is performed to each task according to the longest-period first stack scanned principle. Since the contents of stack may change by each task instance, two factors aid in reducing the additional evacuation and floating garbage produced by garbage collector for periodic tasks: 1) the priori scanning and evacuation of aperiodic tasks 2) longest-period-first stack scanning for periodic mutators since the shorter the period of a task, the higher the possibility of mutation. The global variables tend to be shared and modified by multiple mutators. So, lazy scanning can reduce the overhead of barrier processing. As in [3], instead of using the lazy evacuation technique presented in [4], the garbage collector performs the asynchronous evacuation after the normal evacuation process by maintaining temporary Update Entry. The garbage collector also initializes the new tospace right after the flip, instead of initializing the heap incrementally. The initialization time can be reduced with an efficient hardware support denoted in [3]. Scheduling tasks using multiple serversThe idea of using multiple servers to serve distinct streams of aperiodic tasks was introduced in [10]. There are important reasons why more than one server be desirable in a particular implementation. One reason is that the system contains separate functional components each is best handled by a different server. Another reason is that tasks with different temporal properties are better handled by different servers. Using a single server to process urgent and non-urgent tasks results in poor performance as the urgent tasks are unnecessary delayed by the non-urgent ones specially if the non-urgent is scheduled as high priority tasks [14]. Each server will be assigned a budget, a priority and a replenishment period. Each server is assumed to serve a distinct stream of aperiodic tasks according to the given parameters. The main problem with using multiple servers is how to partition the available capacity among the different servers. When using the non-sharing scheme, this may cause higher capacity exhaustion which will reduce the performance of the server. One busy server can exhaust its budget while the other servers are idle and have capacity. Alan and Bernat in [4] introduced and evaluated a new scheme called the capacity sharing protocol, in which multiple servers share their capacity. This scheme is less sensitive to the specific parameters of the application and hence can be applied to a variety of systems. Whenever a capacity of a server is exhausted, the unused capacity from another server is used. The server to which the server is going to plug is dynamically selected at the time instant when the capacity is exhausted. This will require each server to have a pointer to another server from which the accounting is going to be performed. When the server points to another server, it is called plugged to a host, and the server pointing to the host is called guest server. When the server is running on its own capacity, it is said to be unplugged. There are some rules that govern the sharing protocol [4]:
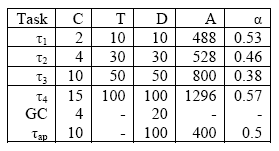
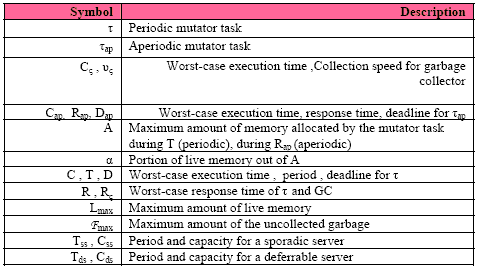
The capacity sharing protocol is equivalent to the single server mechanism when all servers run at the same priority. However, it shows a full preemptive behavior when servers are assigned different priorities. This technique is simple and very easy to implement and has very low memory and computational overhead. 3 SYSTEM MODEL AND ASSUMPTIONThe proposed system model is assumed to be a real-time system composing of four periodic tasks with hard time constraint τ = {τ1, τ2, τ3, τ4} and one aperiodic task (for simplicity) with soft time constraint (τap). The tasks are called mutators, with respect to the GC. The task set (TS1) used is shown in Table 1. Any nomenclature denoted in the paper is provided in Table 2. Each task is characterized by a five-element tuple defined as: (C, T, D, A, α) The underlying assumptions under which the system will operate are as follows: A1 There is only one aperiodic task in the system. It is assumed to arrive at certain time instants: 22ms, 110ms, and 200ms respectively. A2 There is no blocking factor among the tasks. A3 The context switching and scheduling overhead is negligible. A4 C, T, D, A and a for any task (periodic or aperiodic) are known a priori, and the deadline of each periodic task is equal to its period (D = T) A5 Lmax, Fmax, υç are known a priori.
Table 1: The task set (TS1) details
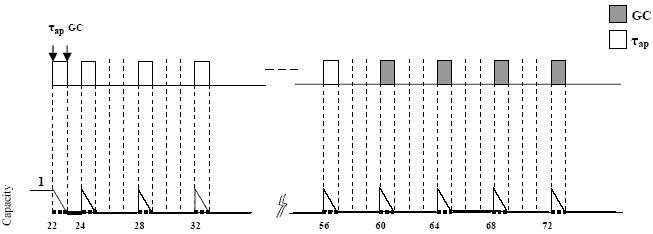
Table 2: The nomenclature used A6 The execution time of GC and that of any periodic mutator task t are in the worst case all along, that is, are always equal to Cç, C. So, is the amount of memory allocated by τ during T. A7 The execution time of any aperiodic task τap is in its worst case all along, that is, is always equal to Cap. So, the amount of memory allocated by τap during Rapsince Rapmay exceed the deadline. A8 Not until the end of one GC cycle can the memory reclaimed in that cycle be available to mutators. A9 For each periodic mutator task τ, the memory consumption behavior repeats periodically, and the consumed memory during one period becomes 'dead' when that period completes. A10 For the aperiodic mutator τap, the memory consumption behavior repeats at each invocation during Rap, and the consumed memory becomes 'dead' at the end of the execution or at the worst-case response time of the aperiodic mutator task. A11 The amount of floating garbage arising during a GC cycle is equal to the amount of garbage generated by mutators during the cycle. A12 For each task (periodic or aperiodic), the amount of memory consumed by it in each time grain is equal to A/C. A13 The GC task arrives at threshold = 3000 The periodic mutators are scheduled by the Rate-Monotonic (RM) scheduling policy described in [11]. This scheduling strategy assigns fixed priorities to tasks according to their periods. The task period is equal to its deadline. The task with the shortest period is given the highest priority in order to minimize the response time of the task to meet its deadline. According to this strategy, if a low priority process is executing and a high priority one is invoked, then the low priority process is preempted and has to wait till the high priority process finishes its execution. When the high priority process finishes, the low priority process can continue its execution unless there is no other high priority task ready to execute. The aperiodic tasks in the system, including the GC thread, are scheduled by distinct real-time scheduling strategies. In all these strategies, only one aperiodic task is assumed to be invoked at selected time instants: 22 ms, 110 ms, and 200 ms respectively during the hyperperiod. They are chosen such that the aperiodic task arrives before one of the GC invocation. This is the worst-case situation that can delay the response time of the GC task upon invocation (i.e. a less urgent or higher deadline aperiodic task arrives before the invocation of the GC task). This may cause the GC to miss its deadline. Accordingly, the system memory requirement increases and hence large areas of memory are required to be able to meet the worst-case situation. GC Scheduling Based On Single ServerUsing one single server to process urgent and less urgent jobs may result in poor performance as the urgent jobs are unnecessary delayed by the non-urgent ones, and the non-urgent ones are scheduled at a high priority [4]. Hence, the GC task may be delayed by a non-urgent task. In this part of work, we aim to explore the behavior of the GC under the given system model which contains an additional aperiodic task. There are two possible types of scheduling. The first one is based on the deferrable server (DS) [19, 20] and the other is based on the sporadic server (SS) [11, 18]. Both techniques have been tested and validated in [11, 18, 19, 20] with a task set containing only periodic tasks while the GC was the only aperiodic task in the system. In the following subsections, we will investigate the performance of DS and SS GC under the proposed system model which its task set contains: a number of periodic tasks, the GC and one aperiodic task. GC scheduling based on single deferrable serverIn this scheduling strategy, the deferrable server task (DS) is used to serve the GC needs like any other aperiodic task in the system. The DS can service an aperiodic task anytime during its period provided that the system still has some unused execution time. This is called bandwidth preserving algorithm. At the end of the DS period, if any portion of the execution time is not used, it is discarded. Figure 3 depicts the operation of the DS GC for the task set arrivals. The DS server's period is taken to be 4ms and the capacity (C ds ) is 1ms as derived in [20]. It is the maximum value that satisfies the schedulability condition for all hard tasks from the exact analysis in [2]. The figure illustrates the worst-case situation that may meet the GC task. We assume that the aperiodic task ( t ap ), which is less urgent and has longer execution and deadline time, arrives before the GC task. At t=22ms, the request for task t ap arrives demanding 10ms. However, just a little bit later, at t = 23ms, a request for the GC task arrives, which only requires 4ms.
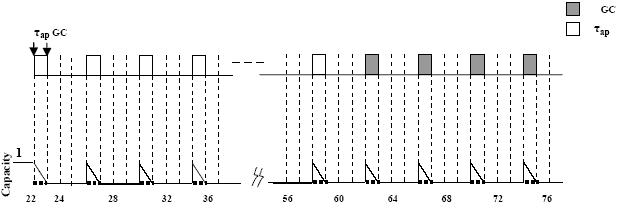
Figure 3. GC Scheduling strategy operation based on single deferrable server for the given task set arrivals (server parameters T=4, C=1) The single server has the problem of effectively scheduling the jobs in FIFO order and it is non- preemptive, making an adequate use of the available capacity. Due to the fact that the server is busy servicing task τap, GC task will have to wait until τap finishes its execution. As the requested execution time for task τap is very long, compared to GC, several replenishments are required to finish its execution. From the figure, we find that τap had a response time of 35ms while its deadline was 100ms. However, the response time of GC was 50ms while its deadline was 20ms despite that it is more urgent and has a shorter requested execution time. Thus, the GC task misses its deadline which will effectively increase the system memory requirement. From the analysis of the given system, it was found that having another aperiodic task in the system beside the GC task could cause the GC to miss its deadline. This can cause serious problems to the system by increasing the system memory requirement. Thus, the performance of the DS GC under this system is under question specially, as we have seen, if the aperiodic task arrived before the GC task. GC scheduling based on single sporadic serverThis scheduling strategy is based on the sporadic server (SS). As in the DS, SS preserves its server execution time at its high-priority level until an aperiodic request occurs. It differs from the DS algorithm in the way it replenishes its server execution time. The DS algorithm periodically replenishes its server execution time to full capacity. The SS algorithm replenishes its capacity one SS period after the arrival of any aperiodic request, and the amount replenished is equal to that consumed by the aperiodic request. SS has the same problem of DS. SS GC also uses FIFO order or SRO queuing policy for scheduling the arriving aperiodic tasks. Figure 4 depicts the operation of the SS GC for the task set arrivals.
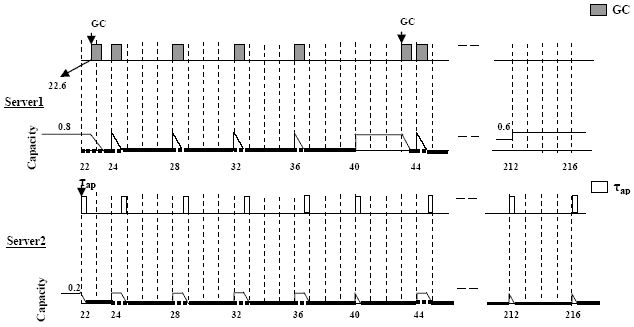
Figure 4. GC Scheduling strategy based on single sporadic server (server parameters T=4, C=1) The SS server's period is 4ms and the capacity (Css) is 1 ms. It is the maximum capacity of the SS server that guarantees that all hard tasks meet their deadlines from [3]. From the figure, it is observed that τap had a response time of 37ms while the GC task had a response time of 52ms which exceeds its deadline (D=20). This will also increase the system memory requirement as in the DS GC. 4 THE PROPOSED GC SCHEDULING BASED ON MULTIPLE SERVERSAs stated in [4], jobs with different temporal properties are better handled by different servers. It seems more adequate to use two servers for GC and τap as they both have different properties. The priority of the server is set up in relation to the urgency of the request; therefore the short and urgent aperiodic request will have a higher priority than the long and less urgent one. Hence, GC task will have higher priority than τap. This scheme is truly preemptive; if the server that handles the long aperiodic request τap is running while GC task arrives; the processor will be immediately switched to GC (the higher priority thread). GC scheduling based on multiple servers is divided into two protocols: without capacity sharing and with capacity sharing. GC scheduling based on multiple servers without capacity sharingFigure 5 depicts the scenario of scheduling the two aperiodic tasks (GC & τap ) with two servers. Each task is scheduled by a separate server. The capacity used previously in the single server has been divided into two budgets (capacities): 0.8ms, 0.2ms. Server1 will have a capacity of 0.8ms and it is assigned to handle GC task while server2 will have a capacity of 0.2ms and it is assigned to handle τap. This assignment was proposed according to the importance of each task.
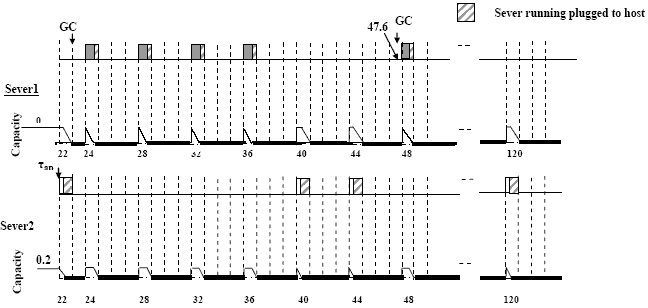
Figure 5. GC Scheduling strategy based on multiple servers without capacity sharing Both servers are DS and will have the same replenishment period of 4ms. According to the scheduling technique without capacity sharing, once the GC task arrives at t=23.6, server2, which was currently running, is preempted. This allows GC task to be served directly upon its arrival without delay. However, server2 now suffers a much longer delay because it has a smaller capacity (0.2ms) than before in single server and therefore will need more replenishment periods to finish its computation. According to this, the response time for τap was 194.2ms which diverges greatly from its deadline while the response time of GC was 14.2ms. Note that if there are other aperiodic tasks, besides the GC task, and are more urgent than the GC, then the server assigned to the GC will have a smaller capacity. This in effect will increase the response time of the GC task. Consequently, the system memory requirement may reach a limit that exceeds the required threshold at the ends of the GC cycles. In this scheme, each server works on its own capacity. The capacity of server1 assigned to handle GC is wasted when the GC task finishes its execution. The scheduling technique without capacity sharing suffers from having missed deadlines for both GC and the aperiodic tasks. GC scheduling based on multiple servers with capacity sharingTo overcome the problems that face the system when the scheduling is based on a single server or multiple servers without capacity sharing, this research proposes to use multiple servers with capacity sharing to schedule the aperiodic tasks. Whenever capacity exhaustion occurs in the servers, the unused capacity from another server is exploited, effectively sharing or stealing it. The capacity sharing protocol considers the partitioned capacity as a common resource that can be shared between the servers. The type of servers used can either be a DS or SS, which yields four possible combinations of both. Figures 6-9 shows the aperiodic tasks scheduling using capacity sharing protocol for the four combinations of server types. The principles discussed in section 2 are applied during the scheduling. From [4], the worst-case response time of all hard tasks is unaffected under a host selection policy that always selects a server with equal or higher priority than the guest server. This means that if there are distinct priorities of the servers in the system and the priorities of hard tasks lie between them then the dynamic selection of the host has to be directed towards a higher priority server than the guest priority in order to maintain the schedulability of hard tasks. In our task set, there are only two servers with the highest consecutive priorities in the system (they have the same configuration as in the protocol without capacity sharing). They can be plugged to each other without any fear on hard tasks schedulability.
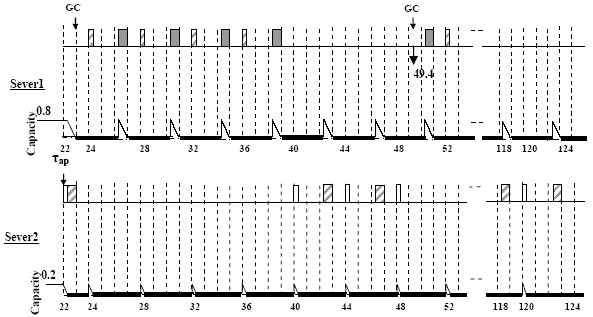
Figure 6: GC Scheduling strategy based on multiple servers with capacity sharing (server1: DS, parameters: T=4, C=0.8, server2: DS, parameters: T=4, C=0.2)
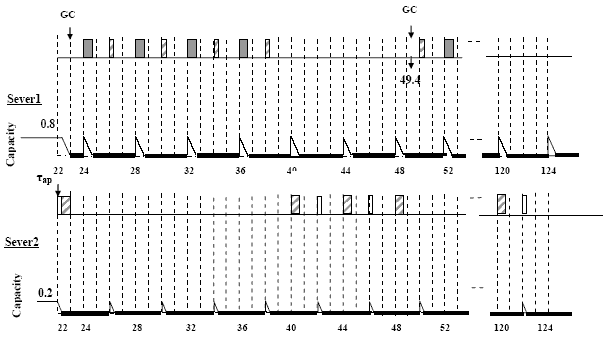
Figure 7. GC Scheduling strategy based on multiple servers with capacity sharing (server1: SS, parameters: T=4, C=0.8, server2: DS, parameters: T=4, C=0.2)
Figure 8. GC Scheduling strategy based on multiple servers with capacity sharing (server1: DS, parameters: T=4, C=0.8, server2: SS, parameters: T=4, C=0.2)
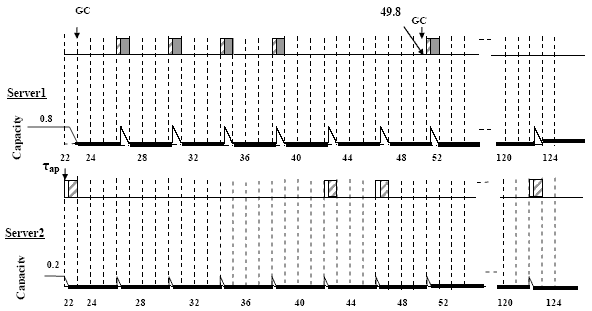
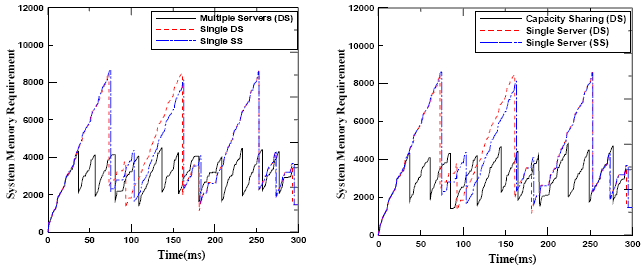
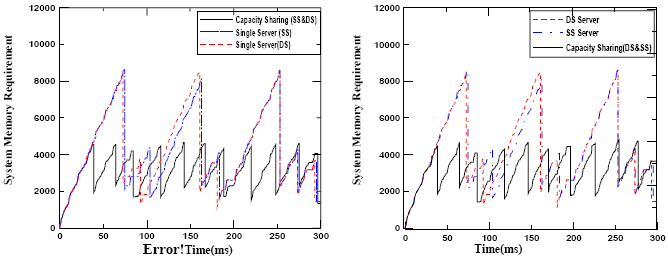
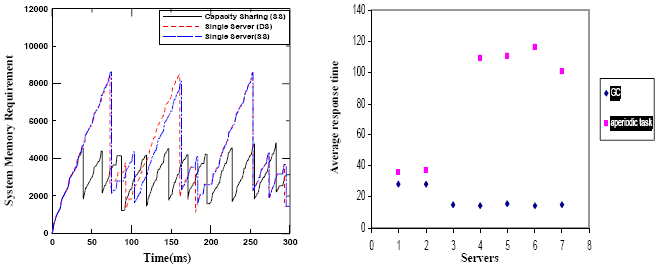
Figure 9. GC Scheduling strategy based on multiple servers with capacity sharing (server1: SS, parameters: T=4, C=0.8, server2: SS, parameters: T=4, C=0.2) In all figures, due to the immediate serving of GC thread upon arrival, it meets its deadline in all situations. Moreover, the response times of t ap were 99,101,100.2,101 ms in Figures 6-9 respectively. The results are very near to the aperiodic task deadline. This means that the scheduling of both GC and the other aperiodic task is better with capacity sharing protocol than with any other method. In the current system, we have two servers at different priorities with no other hard tasks between them. So, we can assign the whole capacity (1ms) to the highest priority server (server1 which is assigned handle to GC task) and none to the other server. With this configuration, GC scheduling based on multiple servers with capacity sharing is equivalent to GC scheduling based on single server but with full preemption as disscused in [4]. 5 SIMULATION RESULTSThis section presents the simulation results of the system memory requirement of the multiple servers with capacity sharing based GC in all its variations against the single server based GC including deferrable and sporadic server. We used the task set (TS1) given in Table 1 and the incremental GC is of the type copying collector. For TS1, C? is 4ms. The GC thread is invoked when the system memory requirement reach the threshold 3000 and the last GC has safely completed. Figure 10 illustrates the contrast of multiple servers without capacity sharing garbage collector (we will call it the multiple servers) and the single server based garbage collector using deferrable and sporadic servers. From the figure, it can be seen that the system memory requirement is reduced when basing the scheduling on multiple servers without capacity sharing. This is using the given capacities of the servers. However, in this task set, there are only two aperiodic tasks; GC which has the higher priority, and τap. The server devoted to serve the GC needs is assigned a capacity of value 0.8 in order to enable the GC thread to meet its deadline at every invocation. However, if there are other aperiodic tasks that are more urgent than GC task then the server responsible for serving the GC needs may be assigned insufficient capacity to enable the GC to meet its deadline. This will increase the system memory requirement since several replenishments occur. Sometimes, at the end of the GC cycle, the system memory requirement may exceed the required threshold and consequently the whole system is crashed. Figures 11-14 compares the proposed strategy that uses the capacity sharing protocol in all its variations to the single deferrable server and single sporadic server based GC. The results show that the scheduling based on the proposed strategy in all its variations outperforms the single server based garbage collectors in minimizing the system memory requirement.
Figure 15 shows the average response times of GC task and t ap for the different types of scheduling. The type of server is denoted by a number where 1: Single DS, 2: Single SS, 3: MS without capacity sharing, 4: MS with capacity sharing (DS), 5: MS with capacity sharing (DS, SS), 6: MS with capacity sharing (SS, DS), 7: MS with capacity sharing (SS). From the figure, it is observed that GC scheduling based on multiple servers with capacity sharing in all its variations aids the GC thread to meet its deadline at every invocation for the task set. The average response time of t ap is also very close to its deadline.
GC scheduling based on multiple servers without capacity sharing also inssures that the GC task meet its deadline but for this task set only. However, the average response time of the other aperiodic task (τap) diverges greatly from its deadline. Thus, the GC scheduling based on single server leads to a very large average response time of the GC task. This occurs as it has to wait till τap finishes its execution to begin. 6 CONCLUSIONSThis paper concentrates on finding a better GC scheduling strategy for embedded real-time systems that contain limited memory size, in the case of having another periodic task in the system. Previous work considered the GC to be the only aperiodic task in the system. Using a single server to serve both GC task and the aperiodic task is not a good policy as both of them have different temporal requirement. The GC task may have to wait till a less urgent request finishes which leads to an increase in the system memory requirement. This research proposes a new concurrent garbage collector based on multiple servers. Two variations of the multiple servers can be used: without capacity sharing and with capacity sharing. The first protocol (without capacity sharing) has a serious problem. The server devoted to GC thread may be assigned a small capacity and since the server works on its own capacity, this may lead to a long response time of GC task as more replenishment occurs. Consequently, this may lead to an overflow in the system memory requirement than the required threshold at GC cycles ends. Thus the second variation is suggested to schedule the GC work via multiple servers with capacity sharing. In this scheme, the partitioned capacity is a shared resource between servers. It is proven through results that scheduling GC based on multiple servers with capacity sharing, whatever the type of the servers used, surpasses single server and multiple servers based garbage collectors in minimizing both the response time of the GC task and the system memory requirement. This is very critical issue for embedded real-time systems. REFERENCES[1] D.F. Bacon, P. Cheng, and V.T. Rajan, A Real-time Garbage Collector with Low Overhead and Consistent Utilization, 30 th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (2003) 285298. [2] D. F. Bacon, P. Cheng, and V. T. Rajan, A Unified Theory of Garbage Collection, ACM Conf. Object-Oriented Programming, Systems, Languages, and Applications (2004) 5068. [3] R. A. Brooks, Trading Data Space for Reduced Time and Code Space in Real-time Collection on Stock hardware, Conf. Record ACM Symposium on LISP and Functional Programming (1984) 256 262. [4] A. Burns and G. Bernat, Multiple Servers and Capacity Sharing for Implementing Flexible Scheduling, J. Real-Time Systems (2002) 49-75. [5] A. Corsaro, and D. C. Schmidt, The Design and Performance of Real-time Java Middleware. IEEE Transactions on Parallel and Distributed Systems 14 (11) (2003) 11551167. [6] M.K. Gardner, and J.W. Liu, Performance of Algorithms for scheduling Real-Time Systems with Overrun and Overload, 11 th EUROMICRO Conf. Real-Time Systems (1999) 287-296. [7] T. M. Ghazalie, and T. P. Barker, Aperiodic servers in a Deadline Scheduling Environment, J. Real-Time Systems (1995) 31-67. [8] R. Henriksson, Scheduling Garbage Collection in Embedded Systems, PhD thesis, Lund University (1998). [9] M. Hertz and E. D. Berger. Quantifying the Performance of Garbage Collection Vs. Explicit Memory Management, ACM Conf. Object-Oriented Programming, Systems, Languages, and Applications (2005) 313326. [10] IEEE Std.10031.d D12 (1999). Draft Information Technology- Portable Operating System Interface POSIX: Part 1: System Application program interface (API) [11] T. Kim, N. Chang, N. Kim, and H. Shin, Scheduling Garbage Collector for Embedded Real-time Systems, ACM SIGPLAN Notices 34 (7) (1999) 55-64. [12] Edward A. Lee, The Problem with Threads, Electrical Engineering and Computer Sciences, University of California at Berkeley, Technical Report No. UCB/EECS-2006-1 (2006) http://www.eecs.berkeley.edu/Pubs/TechRpts/2006/EECS-2006-1.html [13] C. D. Locke, Real-time Java Moving into the Mainstream, RTC Magazine 13 (2004) 6365. [14] Luke K. McDowell, Susan J. Eggers, Steven D. Gribble, Improving Server Software Support for Simultaneous Multithreaded Processors, ACM SIGPLAN Notices 9th ACM SIGPLAN symposium on Principles and practice of parallel programming 38 (10) (2003). [15] M.A. Rivas and M.G. Harbour, Evaluation of New POSIX Real-Time Operating Systems Services for Small Embedded Platforms, 15th Euromicro Conf. Real-Time Systems (2003 ) 161 - 168. [16] S.G. Robertz, Flexible Automatic Memory Management for Real-time and Embedded Systems, Licentiate Thesis, Department of Computer Science, Lund Institute of Technology, Lund University ( 2003). [17] S.G. Robertz and R. Henriksson, Time-Triggered Garbage Collection, ACM SIGPLAN Conf. Language, Compiler, and Tool for Embedded Systems (2003) 93-102. [18] B. Sprunt, L. Sha, and J. P. Lehoczky, Aperiodic Task Scheduling for Hard Real-time Systems, Real-Time Systems (1998) 2760. [19] J. K. Strosnider, J. P. Lehoczky, and L. Sha, The Deferrable Server Algorithm for Enhanced Aperiodic Responsiveness in Hard Real-time Environments, IEEE Transactions on Computers 44 (1) (1995) 7391 [20] Y. Xian and G. Xiong, Minimizing Memory Requirement Of Real-Time Systems With Concurrent Garbage Collector, ACM SIGPLAN Notices 40 (3) (2005). [21] T. Yuasa, Real-time Garbage Collection on General-Purpose Machines, J. Software and Systems, 11 (3) (1990) 181-198. [22] B. Zorn, Barrier Methods for Garbage Collection, Tech.Rep.CU-CS-494-90, University of Colorado, Boulder (1990). About the authors
Dr. Ali Ebrahim El Desokey, Dr. Amany Sarhan, Eng. Seham Moawed: "Using Multiple Servers in Concurrent Garbage Collector", in Journal of Object Technology, vol. 7, no. 4, May-June 2008, pp. 139-158, http://www.jot.fm/issues/issue_2008_05/article4/. |
|||||||||||||||||||||||||