A change propagating model transformation
language
Laurence Tratt, Bournemouth University, Poole, Dorset, BH12 5BB, United
Kingdom
|
 |
REFEREED
ARTICLE
PDF Version |
Abstract
Model transformations are a key component in Model Driven Development, but most
approaches only allow 'one shot' transformations to be expressed. Change propagating
model transformations are those which can make suitable updates to models after an
initial transformation. In this paper I outline the challenges presented by change propagating model transformations, before presenting a new change propagating model
transformation approach.
1 INTRODUCTION
As the use of models - often, but not exclusively, in the form of UML models - in
software development increases, the need for model transformations has increased
[3, 10, 14]. A simple definition of a model transformation is that it is a program which
mutates one model into another; in other words, something akin to a programming
language compiler. Of course, if this simple description accurately described model
transformations, then General Purpose Languages (GPLs) would suffice to express
model transformations. In practise, model transformations present a number of
problems which imply that dedicated approaches are required [18].
In recent times, many different model transformation approaches have been proposed
(see e.g. [9, 7] for overviews of different approaches). Virtually all of these
approaches share in common that they are stateless; that is, after an initial transformation,
the only possible action is to rerun the transformation from scratch creating
an entirely new target model regardless of whether a target model has previously
been created.
In contrast to stateless transformations are change propagating transformations.
Alanen and Porres provide a useful overview of change propagating transformations,
which also explains some of the categories of changes that can be propagated [1]. A
possible scenario is when tools which specialize in different aspects of modelling can
be used together throughout the development life cycle e.g. a UML modelling tool UT and a Java modelling tool JT. In such a scenario, a model is not just transformed
between different tools once, but may be edited multiple times in each tool. For
example, an initial model may be created in UT, transformed and subsequently
edited in JT, before high-level architectural changes are applied in UT which one
expects to see reflected in JT. A similar, although more linear, scenario involving incremental model development is explained in Becker et. al [2]. The general idea
underlying such scenarios is of allowing the user to leverage different tools specialities
at varying points in the development life cycle. In previous work I outlined some of
the other possible uses of change propagating transformations [18].
Currently very little focus has been given to the challenging problem of change
propagating model transformations. To my knowledge, only three approaches tackle
this problem in any way: BOTL [4], Johann and Egyed's approach [12], and XMOF
[6]. All three approach the problem in very different ways, and with varying degrees
of success. From this one can infer that the fundamentals of change propagating
model transformations have yet to be identified.
In this paper I present a new approach to change propagating model transformations
called PMT. PMT is a follow up to my work motivating the need for change
propagating transformations [18], and the unidirectional stateless model transformation
MT [20]. This paper is a condensed version of the technical report [19]
which contains much more detail than the space constraints of journal publication
allow. The aim of PMT has not been to present a definitive change propagating
model transformation approach; rather the aim has been to explore the practical
challenges of implementing a system, and to discover the high-level strategies and
design decisions relevant to change propagation. I believe that PMT offers a number
of insights into the practicalities of change propagating model transformations, and
serves as a solid base from which to build subsequent systems.
This paper is structured as follows. I first give a brief definition of change
propagating model transformations, outlining some generic challenges for any change
propagating model transformation approach. I then describe by example PMT itself.
I conclude by separating out the parts of PMT that are fundamental to change
propagation, thus providing a useful basis for future study of change propagating
model transformations.
2 CHANGE PROPAGATING MODEL TRANSFORMATIONS
A unidirectional change propagating model transformation is considered to consist
of a source model and a target model. Typically before the transformation is first
run, the source model is populated with one or more model elements, and the target
model is empty. After running the transformation for the first time, the target model
is populated with model elements. After this the user may then manually edit both
the source and target models, adding, removing, and altering elements. At some
point the user reruns the transformation and any changes made to the source model
should be non-destructively propagated to the target model. The use of the term
'non-destructive' is deliberate: in propagating changes from the source model, any
manual updates to the target model must be preserved.
This simple description of change propagation does not include a number of the
decisions and challenges that any particular approach must consider. I believe that the following list (though not exhaustive) contains many of the major decisions and
challenges:
Checking or updating propagation. At a minimum, a change propagation approach
may tell the user where changes need to be made to the target model
to make it conformant; at the other extreme an approach may forcibly update
the target model without informing the user of which changes will be made.
Manual or automatic change propagation. [21] outlines a framework where
changes to the source model are extract as change deltas which are then passed
to delta transformations which apply the change delta to the target model. I
term this manual change propagation since a potentially unlimited number of
delta transformations need to be manually written to propagate changes. In
contrast, automatic change propagation is when an approach can propagate
arbitrary changes without manual help. Some systems may use a mix of both
approaches [5].
Batch or immediate propagation. Batch change propagation takes a number of
changes from the source model and propagates them to the target model only
when explicitly requested to do so by the user. The concept of immediate
change propagating transformations is defined in [6]. An immediate change
propagating transformation propagates changes to the target model as soon
as the source model is changed. Unlike a batch mode change propagating
transformation, which implicitly propagates multiple changes when run, an
immediate mode change propagating transformation propagates small changes,
which can be viewed as being semi-atomic.
Relating source and target model elements. All change propagating approaches
require a mechanism that relates (or somehow distinguishes), the specific target
model elements created by a given rule relative to specific source elements.
The distinguishing of elements is vital to ensure that target elements are modified, created or removed correctly during change propagation.
Detecting elements for removal. Removing elements from the source model should
lead to the relevant elements in the target model also being removed (provided
such removals preserve the property of non-destructivity of manual changes).
Checking the correctness of propagation and conflict resolution. Some changes
made to a source model may not be able to be propagated successfully to the
target model. For example, when propagating an element newly added to
the source model, a conflict may arise with an element already present in the
target model.
A lengthier discussion of these items can be found in [19].
3 PMT
PMT is a new approach to change propagating transformations. In terms of the
design decisions enumerated in section 2, PMT can be said to be a fully automatic,
batch, change propagation approach, which relates source and target elements by
their identifiers, and which has user controllable correctness checking built in. The
details of this broad overview will be filled in as this paper progresses. PMT is,
at a low level, a fork of the MT model transformation language [20]; many of the
mundane details of MT apply equally to PMT and are not repeated here. As with
MT, PMT is defined as a DSL within the Converge language [17]. However whereas
MT is in essence an imperative model transformation language, PMT is in essence
declarative.
PMT is interesting for several reasons. As well as being one of the first published
change propagating model transformation approaches, it is the first with a
publicly available implementation. It is also perhaps unusual in that while it is overall
a declarative model transformation approach - where rules define a relationship
between source and target model elements - it is housed within an imperative language,
and rules can themselves contain arbitrary chunks of imperative code. Thus
in PMT the dividing line between imperative and declarative - always somewhat
contentious terms - is extremely blurred.
An overview of PMT
A PMT transformation has a name and consists of one or more rules, the ordering of
which is significant. Rules are declarations, implemented as functions, which define
the source elements they match against, and the target elements that should exist
in the target model given a successful match. Rules are comprised of: a source
matching clause containing one or more source patterns; an optional when clause
on the source matching clause; a target producing clause consisting of one or more
expressions; and an optional where clause for the target production clause.
A PMT transformation takes in one or more source elements, which are referred
to as the root set of source elements. The transformation then attempts to transform
each element in the root set of source elements using one of the transformations rules,
which are tried in the order they are defined. If a given element does not cause any
rule to execute then an exception is raised and the transformation is aborted. The
general form of a PMT transformation is as follows:
The import statement is a normal expression in the Converge language and imports
the MT module. DSL blocks are introduced by $<<...>> - in this example an PMT
model transformation DSL block. Since Converge is an indentation based language,
all code indented from the $<<MT.mt>> line is part of the DSL block; note that
code preceding $<<MT.mt>> is normal Converge code, as is any code following the
DSL block. As this example shows, a Converge DSL can conform to an arbitrary
grammar. A DSL block is translated into a Converge abstract syntax tree using
Converge's compile-time meta-programming facilities. Arbitrary Converge code can
be embedded inside the DSL block itself (see [17, 20] for more details on these
mechanisms).
The srcp and srcp_when clauses are collectively said to form the source clauses;
similarly the tgtp and tgtp_when clauses are collectively said to form the target
clauses. Transformation rules contain normal Converge code in expressions; such
expressions can reference variables outside of the model transformation DSL fragment.
Users can thus call arbitrary Converge code, allowing them a means to extend
the model transformation approach as necessary. This is an important aspect of
PMT since it allows users to use normal Converge functions arbitrarily, and without
penalty; this stands in contrast to many model transformation approaches which
provide a 'closed world' which can not easily be extended.
Pattern language
PMT's pattern language is a super-set of that found in the QVT-Partners approach.
PMT defines a number of pattern expressions: model element patterns, set patterns,
variable bindings, and normal Converge expressions. Model element patterns are
of the form (Class, <self_var >)[slot name == pattern]. A model element
pattern matches against a model element of type Class, and then checks each slot
comparison slot name against a pattern pattern. If the type check, or any of the
slot comparisons, fails then the entire model element pattern fails. In general, any
of the standard Converge comparison operators (e.g. ==, >= etc.) can be used in slot
comparisons, and the same slot name may be involved in multiple comparisons in
any given model element expression. If the type of the model element pattern, or any
slot comparisons, fail then the model element pattern itself fails. Set patterns are
directly analogous to those found in functional languages such as Haskell. Variable
bindings <v> intuitively mean 'match anything and bind to v'. If the same variable
binding appears more than once in the same scope, all instances of that variable
name must match against equivalent objects (the QVT-Partners approach does not define its own notion of equality, instead inheriting it from the MOF [15]). Converge
expressions, when used as patterns, match only against a model element which
compares equal to the evaluated Converge expression. If a model element expression
successfully matches against a model element, then the model element is bound to
the optional self variable self_var.
As a trivial example of a model element pattern, assuming an appropriate metamodel,
the following example will match successfully against a Dog model element
whose owner is not Fred, binding the matching Dog element to the variable d and
its name to n:
Execution strategy
PMT can execute as both as both a full and semi-conservative updating propagation
approach, and the two modes can be arbitrarily intertwined. When PMT is executing
in fully conservative mode, it forcibly propagates only those changes which
do not interfere with any existing target model elements; in semi-conservative mode
it attempts to forcibly propagate all changes. In both cases, the overall execution
strategy is the same: PMT executes, attempting to make the source and target
models conformant with respect to each other and the transformation.
The use of the phrase 'make the source and target models conformant with
respect to each other and the transformation' is deliberate: a PMT transformation
is essentially a constraint, and for any given transformation and a particular source
model there may potentially be many conformant target models (and vice versa).
Making a target model conformant may require elements being added, altered, or
removed from the target model. The way in which the relationship between source
and target elements is specified, and the process by which the update of the target
model occurs are the two defining aspects of PMT.
A PMT transformation's stages
The stages of a PMT transformation are as follows:
- Take a source model, and an empty target model and transform the source
model. This stage - if taken in isolation and viewed as a black box - is simply
that of a standard unidirectional model transformation. After the transformation
has executed, the source and target models, together with tracing
information created, are stored in some fashion.
- The user may make arbitrary changes to both the source and target models,
independent from one another.
- The user then requests that the changes they have made to the source model are propagated non-destructively to the target model. The transformation
is reinitialized with the updated source and target models, and the tracing
information from the previous execution. The execution of the transformation
then propagates changes from the source model to the target model. After the
transformation has executed, the source and target models, together with the
new tracing information created are once again stored.
At this point, the sequence moves back to stage 2.
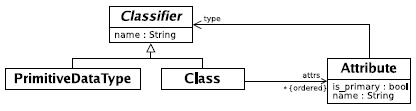
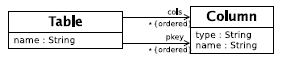
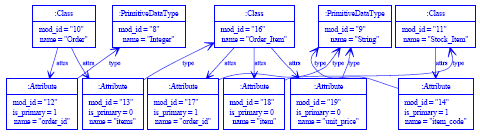
4 EXAMPLE
The example I use in this paper is a version of the standard 'class to relational model'
transformation [16], reduced in complexity in the interests of brevity. The 'Simple
UML' meta-model is shown in figure 1, and the relational database meta-model in fi gure 2. Essentially each class is translated to a table. One or more of a classes
attributes must be marked as being part of its primary key; attributes either have
a primitive (e.g. integer, string) type or refer to another class for their type; if an
attributes' type is that of another class, the primary key of that class is used as a
foreign key (recursively, and possibly spanning multiple columns).
Figure 1: Extended 'Simple UML' meta-model.
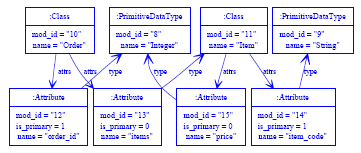
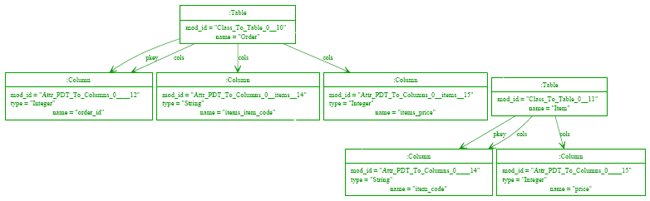
Figure 2: Extended relational database meta-model.
The transformation itself is as follows:
The overall structure of this transformation is hopefully relatively straightforward
even if some of the finer details are not. The Class To Table rule ensures that each
class transformed into a table in the target model. Attr PDT To Columns transforms
an attribute with a primitive type into a single column. Attr Class To Columns transforms an attribute whose type is another class into one or more columns, building
up the prefix of the eventual column(s) name. concat name(p, n) is a normal
Converge function which concatenates the string p with n (separating the two by an
underscore) if p is empty, otherwise returning n.
Three features in this transformation need extra explanation in the context of
this paper. First, the self variable in Converge code is analogous to this in Java
| PMT transformations are in fact translated to a Converge class, and one can thus
access specific rules and so on via the self variable. Second, the transform function
used throughout the transformation is also present in every PMT transformation.
It takes an element(s) in, and successively tries every transformation rule in the
transformation using the arguments passed to it, attempting to find one which
executes given the element(s) as input. If no rule executes, the transform function
raises an error. The transform function is used internally by PMT to transform
each element in the root set but, as in this example, may be called at will by the
user. Third the for keyword in target pattern of the Attr_Class_To_Columns rule is used to generate multiple target elements; essentially for each time time that
the expression on the right hand side of the for expression evaluates successfully
(using the standard Converge semantics), a new target element will be created.
Example execution
Figures 3 and 4 shows the automatic visualization of a source model and resulting
target model from running the transformation of the previous section, in UML object
diagram format. The relationship between source and target is simple at this stage;
the main detail to note is that source models are always presented in blue, and
target models in green.
Figure 3: Source 'Simple UML' model.
Figure 4: Target relational database model.
At this point, we make the following changes to the source and target models:
we rename the Item class to Stock_Item; remove the items attribute from Order,
replacing it with a Order_Item class that can track changing stock prices over time;
and we change the name of the Order table in the target model to Cust_Order.
The source model at this point looks as in updated source simple UML model.
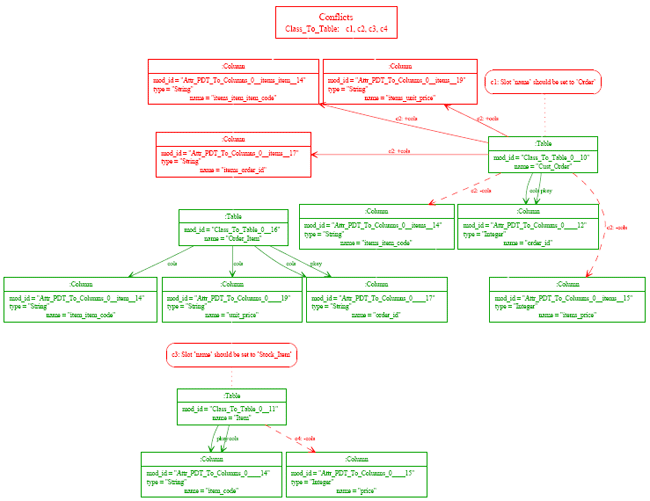
Figure 5: Updated source 'Simple UML' model.
After re-running the transformation, the target model looks as in 6. The obvious
difference in figure 6 is the large number of model elements in red, which denote conflicts. The reason for these red elements is that the transformation defined in
section 4 is a fully conservative transformation. When the transformation is run
(initially or subsequently), it attempts to transform source elements; those which
it can transform without interfering with pre-existing target model elements are
transformed (hence the appearance in figure 6 of the new Order_Item table). Those
source elements which would interfere with pre-existing target model elements are
labelled in red.
In the following subsections I go into more detail about conflicts, how PMT
relates source and target model elements, and how PMT transformations can be
turned from semi-checking into updating change propagation approach.
Figure 6: Updated target relational database model.
Conflicts
Figure 6 shows a number of model elements in red. Elements and links shown
with solid red lines are those which need to be added to the target model in order to
make it conformant; elements and links shown with a dashed red line to be removed.
Boxes with rounded corners are informational (saying that a particular slot in an element needs to be changed and so on). Collectively these conflicts constitute what
can be thought of as a visual 'diff' [11]; if all of the changes indicated are made,
then the source and target models are conformant with each other relevant to the
transformation.
There is also other interesting, and sometimes important, information that can
be gleaned from figure 6. At the top of the figure is a legend box which records which
rules led to conflicts being generated; it is deliberately similar to the visualization
of traces in the MT model transformation language [20]. In the case of figure 6, one
can see that four separate executions (labelled c1 to c4) of the Class_To_Table rule led to conflicts. Each conflict in the diagram itself is labelled with one of these
executions; as can be seen from execution c2, multiple conflicts may result from
one execution of one rule. By looking at the execution number on an element or
link, one can determine not only which rule led to the conflict, but whether other
elements were involved in the same execution of that rule.
One question raised by figure 6 is: why are two cols links from the Cust_Order element in dashed red, but not the elements to which the links point? This is tackled
in section 5.
Relating source and target model elements
Up until now I have been deliberately vague as to how PMT knows which source
and target elements are related to each other. There are three main ways that one
can imagine determining this relationship: by key, by tracing information, and by
identifier. In this section I briefly outline these mechanisms, before discussing PMTs
approach to relating elements.
Element relation mechanisms
The three main mechanisms for relating elements, and their pros and cons, can be
summarised as follows:
Relating elements by key This involves relating elements by a collection of attributes
which, collectively, uniquely identify any given element (as in the
standard database notion of key) and is advocated by the DSTC QVT approach
[8]. Transformations thus only need to know about the relation of
source and target element keys; other information in model elements is essentially
irrelevant.
There are two problems with this method. The first is that by requiring models
to define keys, an extra burden is placed on the user. Although this is often
trivial, it can be difficult when elements have no natural key. The second is
more fundamental, and relates to the fact that, after the initial transformation,
the user can not safely change source or target elements keys since changing a
keys value means the transformation may no longer correctly relate elements. Relating target elements via tracing information Tracing information relates
which source elements led to the creation of particular target elements. As this
information is created by PMT already - PMT uses the same tracing creation
scheme as [20] - it seems like a good candidate to relate source and target
elements. However, as shown in [20], there are various different tracing information
creation mechanisms. The success of a change propagation algorithm
then depends on factors such as the coverage and granularity of the recorded
tracing information. For example, while the default tracing information generated
by PMT records which target elements were created by a rule from
specific source elements, it does not generate enough information to know
which part of the rule created which target element. Such information may be
vital for an accurate change propagation algorithm.
There is thus a potential tension between the different uses of tracing information.
The type of tracing information desirable for change propagation may
be very different from that required by a user to understand transformations
on their model. However, assuming that it is suitably detailed, tracing information
is sufficient as the sole means of distinguish elements for change
propagation. Distinguishing target elements by identifier A technique that can ultimately
be seen as a slight variation on distinguishing target elements by tracing information
was outlined by Johann and Egyed in [12], and independently by
this author in [18]. When a target element is created it is given an identifier
which contains, at a minimum, the concatenated identifiers of all the source
elements which led to the creation of the target element. Henceforth I refer
to this as the target element identifier. Note that the target element identifier
may be in addition to an elements standard identifier, and that conceptually
there is no requirement that this new identifier be a single field.
Conceptually this technique does not add any additional power over using
tracing information to distinguish elements. Indeed, a simple concatenation
of the source elements identifiers means that the target element identifier is
merely an alternative way of storing information that can in theory be directly
derived from suitably fine-grained tracing information. However extra
information can be easily stored in the target element identifier, if required,
to allow a transformation to encode information which may not be present in
tracing information. This then allows tracing information to be used for other
purposes. Furthermore this then means that tracing information need neither
have complete coverage, nor be fine-grained; as such, tracing information can
be recorded in a fashion which gives it the greatest utility to the user.
PMTs approach to relating elements
Since it is the approach with the least cons, PMT distinguishes target elements by
identifier. In simplified terms, a rule concatenates together the identifiers of the
source elements it has matched, and then sees if an element with such an identifier
already exists in the target model. If no such element exists, PMT creates a new object.
However if such an element exists, it is used as the basis for further operations.
Creating suitable target element identifiers is thus a significant part of PMT.
Fundamentally target element identifiers need to satisfy two criteria: that they
are unique with respect to particular source elements and a particular rule execution;
that they can be created deterministically across multiple transformation executions
to allow changes to be propagated multiple times. In order to satisfy these two
criteria, PMTs approach to creating identifiers is somewhat more sophisticated than
has been suggested, or indeed described in previous publications.
From a purely implementation point of view, PMT uses the mod id field in model
elements to store identifiers. As can be seen from e.g. figure 6, this field stores
a string. By default each new model element is given a unique string identifier
(a number starting from 0 and monotonically increasing when a new element is
created), but new model elements can be assigned an arbitrary model identifier.
Concatenating the identifiers of source elements is not sufficient on its own to
generate unique target element identifiers, since the same source elements may be
used in more than one rule execution. PMT thus also integrates the name of the
rule being executed into the target identifier to ensure that target element identifiers
are unique. This is sufficient when a rules target clauses contain a single model
element expression which executes only once. If a rule has multiple model element
expressions in its target clauses, or if a model element expression can execute more
than once in a single execution of a rule, then a single target element identifier
might result in multiple target elements being created with the same identifier. In
order to ensure uniqueness, each rule execution keeps a counter of how many times
model element expressions have been executed during the execution. This counter
is incorporated into the target element identifier of model element expressions, thus
ensuring the uniqueness of the identifiers even when a rule executes more than one
model element expression.
The general form of a target element identifier in PMT is thus as follows:
Using this template, one can interpret the identifiers of target elements in figure 6
with respect to the transformation of section 4.
There is one last potential cause of conflict in the generation of target model
identifiers: executing the same rule with the same source elements more than once
could lead to conflicting target identifiers being generated. To avoid this possibility,
PMT rules keep a cache of source elements that have already transformed: if a rule
matches against the same source elements as it did in a previous execution, then the
target elements produced in that previous execution are returned. Note that this
design decision is vital to ensure the uniqueness of model element identifiers.
5 EXTENDING THE EXAMPLE
The example presented in section 4 showed a transformation executing in fully conservative
mode. In this section I show how PMT can execute in semi-conservative
mode, that is PMT attempts to forcibly propagate all changes. In order to do this
we have to make changes to the transformation itself. The updated transformation
is as follows:
The only changes made to this updated transformation are in the model element expressions in the target clauses of rules. Previously it was possible to think of
both source and target clauses containing patterns; indeed PMT's syntax has been
deliberately designed to encourage this. However it is now necessary to differentiate
the purely matching model element patterns in source clauses from the constructive
- and potentially updating - model element expressions in target clauses. Where
before each slot comparison (see section 3) in model element expressions was ==,
conformance operators such as the following can be used in model element expressions:
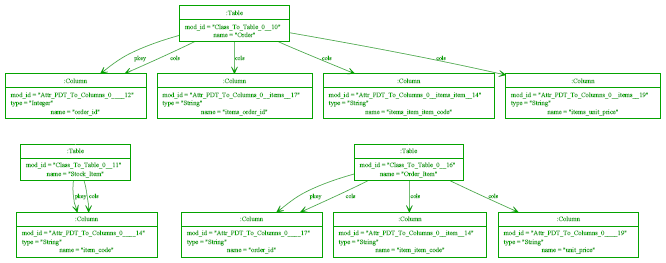
Running this new transformation on the source model of figure 5, the resultant
target model is figure 7. The most obvious feature of figure 7 is that there are now
no elements in red - all the conflicts of figure 6 have been automatically resolved.
Figure 7: Target model after changes propagated.
The execution strategy for transformations using conformance operators such as
those listed above is exactly the same as before. As the transformation executes, it
attempts to make target model conformant to the source model and itself by adding
or altering elements as needed. If it is unable to make an element conformant, it is
possible for conflicts to be raised in the same style as before, although it is rare to
hit such cases in practice.
It is easy to assume that the conformance operators above are really just imperative
updating expressions in disguise. However conformance operators such as :>= have both updating and constraint properties, that are vital for change propagating
transformations. Taking figures 5 and 7 as a basis, let us assume that the user has
added an attribute Address of type String to the target class Order, and a column total of type String into the target table Order. Having made these changes, and
running the transformation again, an elided version of the target model can be seen
in figure 8. Not only has the address attribute change been propagated into the
target model, but the manually added total column has been left untouched.
The update superset conformance operator is particularly interesting since it does
not imply, or force, the value of the slot in the target element to be directly equal
to the value generated by the model expression. Instead, the value of the slot in the target element is altered to make sure it contains all the elements that the model
expression says it should have; if it has extra elements then those are left intact. I
believe this ability to non-destructively propagate changes - i.e. to leave manually
modified elements of the target model alone when they do not conflict with the
transformation - is vital for real-world change propagating transformations. Note
that although PMT contains several other conformance operators, the := and :>= are by far the most commonly used in practise.
Figure 8: An elided version of a user-modified target model after changes propagated.
One important point that may not be immediately obvious is that transformation
writers still need to use careful thought to determine when each should be used. For
example, an inexperienced transformation writer may choose to use the update
operator in all slot conformances, since this will ensure that all changes made to the
source model are propagated automatically to the target model. However if the slot
in question contains a set then the users' manual changes made in the target model
will be destroyed. In such cases, one would generally expect the transformation
writer to use the updating slot conformance operator. In some cases, however,
the transformation writer may deliberately wish to ensure that the target model
contains the transformed set elements, and nothing else, in which case the update
conformance operator is the correct choice. Knowledge of the appropriate situations
for each conformance operator is likely to be gathered only through knowledge of the
source and target domains, and experience with the change propagating approach.
Removing source elements
Removing elements from the source model poses a special challenge to change propagation.
As explained previously, PMT's approach to propagating changes has always
been to propagate new or changed source elements to the target model. If the user
removes an element from the source model, one would expect the appropriate element(
s) to be removed from the target model on propagation. This requirement
may at first appear to be solved by examining all target elements at the end of a
transformation execution, and removing those elements which were not created as
the direct result of transforming one or more source elements. However this simple
solution would also delete any elements manually added to the target model by the
user, and as such is clearly not suitable for the use cases PMT is aimed at. The
critical problem is therefore to distinguish which seemingly superfluous elements in
the target model have been manually added by the user, and which are no longer a
part of the transformation.
In order to determine which elements can be safely deleted in the target model,
PMT utilises tracing information - both that generated by an execution of the transformation,
and that generated by its previous execution. After changes have been
propagated, a PMT transformation examines every element in the target model,
checking whether it is referenced in either or both of the current and previous tracing
information. Based on this, PMT draws a conclusion about the origins of the
element and whether it is a candidate for removal. The four possibilities for an
element are as follows:
Once every element has been examined, PMT performs a garbage collection
style 'mark and sweep' [13], using the transformed root set of source elements as the
starting point. Any self-contained cycle consisting solely of elements marked as being
candidates for removal, is then removed from the target model. The need to identify
self-contained cycles of such elements is to prevent the removal of elements cause
the target model to become ill-formed. This could occur if elements are removed
from the model even though they are referred to by other objects.
6 RELATED WORK
Only three model transformation approaches are of potential interest with respect
to change propagation: BOTL [4], Johann and Egyed's approach [12], and XMOF
[6].
BOTL restricts itself to bijective transformations which is extremely limiting as
the majority of real-world transformations fail to satisfy either or both of the injective
(commonly known as 'one-to-one') and surjective (commonly know as 'onto')
criteria that this requires.
The XMOF approach is interesting in that it uses full constraint solving to tackle
the problem of bidirectional change propagating model transformations. However
bidirectional transformations - stateless or change propagating - introduce significant
extra complexity into the transformation process. There are two issues with
XMOF that make it rather difficult to use. First, by its very nature, and even
with perfectly specified systems, it can take an unbounded amount of time to solve
constraints and execute. Second, it places a significant burden on the user to make
sure that the constraints they specify completely describe the transformation - if
they fail to do this, the resulting transformation is likely to either produce arbitrary
results each time it is run, or to run out of memory as it attempts to enumerate all
matching values.
Johann and Egyed's approach is the most interesting of the three, and the closest
in spirit to PMT, as it tackles unidirectional change propagating model transformations;
however it explains only one aspect of its approach in detail, and furthermore
is incapable of correctly propagating some important types of changes. Specifically,
the approach attempts to optimise propagation so that only updates local to the
change are propagated. As shown in [19], local changes sometimes have global effects
on the transformation. Because PMT effectively performs a full transformation
every time it propagates changes, it can correctly propagate such changes.
7 LIMITATIONS AND FUTURE WORK
Although PMT is successful in many ways, as a first-generation change propagating
approach, there are several directions in which future work could usefully go. For
example, it might be possible to optimise many simple types of changes so that
only a subsection of the transformation is rerun; [19] has more some more concrete
suggestions along these lines.
Looking in a completely different direction, PMT fundamentally works on the
basis of continually updating the target model. An interesting area of research
would be for PMT to change to producing diff's against the target model (as in
section 4), keeping a complete history of such diffs. This would allow the target
model to be manually manipulated by the user, who could choose which aspects
of which diffs to include at any given point, in analogous fashion to textual version
control systems. By keeping a history of diffs, PMT might also be able to make more
intelligent decisions about element deletion by taking into an account an elements
entire history.
8 CONCLUSIONS
In this paper I have presented the PMT change propagating model transformation
language. I explained in detail how PMT approaches the task of change propagation.
My aim in this has not been to present PMT as the definitive change propagating model transformation approach; rather it has been to explore some of fundamentals
of change propagation, to show workable design decisions for a resulting system, as
well as to show how it works in practise. I therefore hope that PMT's approaches to
transformation execution, target element identifiers, conformance operators, element
removal and so on serve as a useful reference for future transformation users and
language authors.
This research was funded by a grant from Tata Consultancy Services.
REFERENCES
[1] M. Alanen and I. Porres. Change propagation in a model-driven development
tool. Presented at WiSME part of UML 2004, October 2004.
[2] S. M. Becker, T. Haase, and B. Westfechtel. Model-based a-posteriori integration
of engineering tools for incremental development processes. SoSYM, 2004.
To appear.
[3] J. Bézivin and S. Gérard. A preliminary identification of MDA components. In
Generative Techniques in the context of Model Driven Architecture, Nov 2002.
[4] P. Braun and F. Marschall. Botl - the bidirectional object oriented transformation
language. Technical Report TUM-I0307, Institut für Informatik der
Technischen Universität München, May 2003.
[5] Compuware. OptimalJ, 2004. http://www.compuware.com/products/optimalj/.
[6] Compuware and Sun. XMOF queries, views and transformations on models
using MOF, OCL and patterns, August 2003. OMG document ad/2003-08-07.
[7] K. Czarnecki and S. Helsen. Classification of model transformation approaches.
In J. Bettin, G. van Emde Boas, A. Agrawal, E. Willink, and J. Bézivin, editors, Second Workshop on Generative Techniques in the context of Model Driven
Architecture, October 2003.
[8] DSTC, IBM, and CBOP. MOF query / views / transformations first revised
submission, August 2003. OMG document ad/2003-08-03.
[9] T. Gardner, C. Griffin, J. Koehler, and R. Hauser. Query / views / transformations
submissions & recommendations towards final standard, August 2003.
OMG document ad/03-08-02.
[10] A. Gerber, M. Lawley, K. Raymond, J. Steel, and A. Wood. Transformation:
The missing link of MDA. In A. Corradini, H. Ehrig, H.-J. Kreowski, and
G. Rozenberg, editors, Graph Transformation: First International Conference,
ICGT 2002, pages 90-105, October 2002.
[11] J. Hunt and M. D. McIlroy. An algorithm for differential file comparison.
Technical Report 41, Bell Laboratories Computing Lab, July 1976.
[12] S. Johann and A. Egyed. Instant and incremental transformation of models.
September 2004.
[13] R. Jones and R. Lins. Garbage Collection: Algorithms for Automatic Dynamic
Memory Management. Wiley, 1999.
[14] E. Kapsammer, T. Reiter, and W. Schwinger. Model-based tool integration -
state of the art and future perspectives. In Proc. CITSA 2006, July 2006.
[15] Object Management Group. Meta Object Facility (MOF) Specification, 2005.
formal/05-05-05.
[16] QVT-Partners. First revised submission to QVT RFP, August 2003. OMG
document ad/03-08-08.
[17] L. Tratt. The Converge programming language. Technical Report TR-05-01,
Department of Computer Science, King's College London, February 2005.
[18] L. Tratt. Model transformations and tool integration. Journal of Software and
Systems Modelling, 4(2):112-122, May 2005.
[19] L. Tratt. A change propagating model transformation language. Technical
Report TR-06-XX, Department of Computer Science, King's College London,
August 2006.
[20] L. Tratt. The MT model transformation language. In Proc. ACM Symposium
on Applied Computing, pages 1296-1303, April 2006.
[21] L. Tratt and T. Clark. Issues surrounding model consistency and QVT. Technical
Report TR-03-08, Department of Computer Science, King's College London,
December 2003.
About the author
Cite this article as follows: Laurence Tratt: "A change propagating model transformation language", in Journal of Object Technology, vol. 7, no. 3, March-April 2008, pp. 107-126, http://www.jot.fm/issues/issue_2008_03/article3/
|
