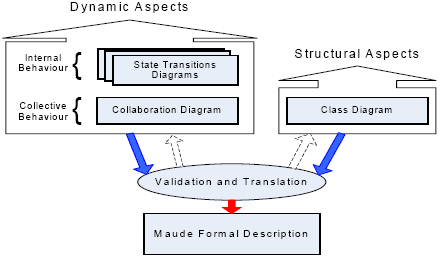
AbstractWe present, in this paper, a framework supporting a formal verification of concurrent UML models using the Maude language. We consider both static and dynamic features of concurrent object-oriented systems. We focus on UML class, state and communication diagrams. The formal and object-oriented language Maude, based on rewriting logic, supports formal specification and programming of concurrent systems, as well as model checking. The major motivations of this work are: (1) translating concurrent UML diagrams into a Maude formal specification and (2) applying model checking to the generated specifications. The approach is illustrated using a concrete case study.1 INTRODUCTIONUML ( Unified Modeling Language ) is a language for specifying, visualizing and constructing the artifacts of software systems [OMG05]. Nowadays, it is considered as the standard for object-oriented modeling. UML allows modeling various aspects of complex systems. However, UML models can present some ambiguities and inconsistencies as mentionned in several papers [Bruel00, Jean-Pierre05, Barnett04, Taibi03, Gallardo02]. UML suffers, in fact, from a lack of formal semantics [Astesiano98, Reggio04, Taibi03]. This weakness can lead to inconsistencies within the developed models. Using formal methods, particularly in the case of complex systems, presents notable advantages [Bruel00, Gallardo02, Taibi03, Meseguer03, Bowen03], like a simpler design without ambiguities, as well as a more complete documentation [Bowen03, Taibi03]. Concurrent programming is a powerful paradigm where activities can be executed concurrently [Garcia02, Gomaa00]. However, this way of programming has its specific problems. Concurrent threads executing on the same resources can lead to unwanted and unexpected situations. For example, deadlocks, livelocks or data inconsistencies may occur [Garcia02, Gallardo02]. In [Wegner90], Wegner describes the general concept of active objects. Contrary to usual objects, which are activated when receiving a message, active objects may be already executing when receiving a message. Therefore, these objects have at their disposal a message queue. Wegner also discusses the concepts of internal and external concurrency [Wegner90]. When discussing external concurrency, we mean two active objects executing on the same resource. Those active objects can have a single thread, therefore sequential. A quasi concurrent active object is an object for which the internal behavior shows concurrent features. Finally, a fully internal concurrent active object has several threads of execution. In this paper, we mainly focus on external concurrency, as two objects attempt to access the same resource. Furthermore, Model Checking is a type of formal methods using a usually abstract model of a system to determine whether a series of properties are satisfied about that system [Chan98a, Chan98b, Cho99, Gallardo02, Merz00, Merz01, Lam04]. According to Gallardo & al. [Gallardo02], Model Checking is one of the most useful results of research in formal methods to increase the quality of software. A model checker is an automatic tool that compares two descriptions of the behavior of a system, one being considered as the requirement and the other the actual design [Gallardo02]. The main usefulness of such a technique is the fact that the automatic tool, upon encountering an error state, returns a counterexample illustrating the path taken to reach that state [Gallardo02, Merz00, Merz01, Lam04]. However, Model Checking suffers from a major problem, known as the state space explosion problem [Gallardo02]. Since a model checker confirms the validity of a given property by an exhaustive analysis of all execution paths, the state space can become very big very soon. Several solutions to this were proposed, for example symbolic model checking, abstraction, or on-the-fly analysis [Merz00, Wahl03]. In this paper, we present a formal framework supporting: (1) the translation of UML diagrams into a formal specification based on the Maude language and (2) the verification of some LTL properties using Maude's integrated model checker. We consider both static and dynamic features of concurrent object-oriented systems. We focus, in particular, on UML class, state and communication diagrams jointly. The approach is organized in four major steps. The first step consists of describing both static and dynamic features of an object-oriented system using UML class diagram (static structure), state (individual behavior of objects) and communication diagrams (collective behavior in terms of dynamic interactions between objects). The second step corresponds to an inter-diagrams validation process. The third step consists of automatically generating a Maude description from the considered UML diagrams. The fourth step consists of verifying some LTL properties using Maude's model checker [Eker02, Meseguer03, Clavel05]. We focus, in this paper, on applying Maude model checking techniques to concurrent UML diagrams. The translation process has been addressed in a previous paper [Mokhati06], but was subject of an extension to consider the particularities of concurrent object-oriented systems for both internal and external concurrency. The remainder of the paper is organized as follows: In Section 2, we give a brief overview of related work. Section 3 briefly presents the UML diagrams we consider. Section 4 gives an overview of rewriting logic and Maude. We present, in Section 5, the main phases of the translation process and illustrate it using a concrete case study in Section 6. Section 7 presents how Maude's model checker can be used to verify LTL properties. Finally, we give a conclusion and some future work directions in Section 8. 2 RELATED WORKFunes & al. [Funes02] have formalized UML class diagrams using the formal specification language RSL ( RAISE Specification Language ). Using the same language, Meng & al. [Meng04] presented a formalization for state diagrams. Furthermore, Favre [Favre05] has proposed a translation process for class and package diagrams in the NEREUS language, based on the MDA (Model Driven Architecture) methodology. The obtained NEREUS specification is transformed into an object-oriented code ( Eiffel language). Joao & al. [Araujo00] proposed a generation process to obtain Object-Z specifications from UML communication diagrams. In the same context, other UML diagrams have been considered [Dong00, MacColl99]. On the other hand, Paige and Brooke presented in [Paige04] a pragmatic approach integrating the object-oriented methodology BON (an alternative to UML) and the Object-Z language. Their approach was implemented using the BON-CASE tool [Paige02]. This tool supports formal specifications through pre-conditions, post-conditions and class invariants, whether for reasoning or for formal analysis [Paige02]. The majority of these papers have focused on translating to a formal specification only one feature of object-oriented systems, whether static or dynamic. In the same context, other approaches have considered jointly class diagrams to describe static aspects of object-oriented systems and state diagrams to describe their dynamic aspects (individual behavior of objects). We can cite, among others, the U2B tool [Snook04]. U2B is a script file for Rational Rose that allows the conversion to the B language the Rational Rose model composed of class and state diagrams. However, the collective behavior of objects, in terms of dynamic interactions between objects, is not considered. Furthermore, H. Ledang & al. have developed the ArgoUML+B tool [Ledang03, Tigris02]. Of course, those proposals have considerably forwarded the domain by integrating static and dynamic features of object-oriented systems and their translation into formal specifications. However, the dynamic features considered in those papers, jointly to the static features, are only related to the individual behavior of objects. The collective behavior is not addressed. Model checking issues are nowadays a very active research domain. Several tools are offered to assist developers in such a task. Some of those tools also support the formal verification of concurrent systems. SPIN is one of the most renowned model checkers available. It has been used in several works. In [Merz01, Merz00], SPIN has been used to model check state machines and collaborations together, and more particularly concurrent state machines using concurrent regions of a superstate. Their approach consists of verifying that the collective behavior of the objects specified by the collaboration diagram can be satisfied by a set of state-transition diagrams. The authors developed a tool called HUGO which compares the state charts descriptions defined in PROMELA, the input language of SPIN, to textual representations of collaborations. HUGO then uses SPIN to complete its verifications. This approach, however, does not integrate the structural aspects of the system. In [Canals03], the authors present a tool, called NEPTUNE, which contains a module, called Checker, supporting the verification of UML models including some properties expressed using the OCL language. Furthermore, the tool BON-CASE [Paige02, Paige04] contains a reasoning engine which allows the verification of different properties, which is comparable to NEPTUNE. In [Chan98a, Chan98b], the authors used the RSML language (which is an alternative to UML to represent state charts) to formalize the TCAS II program (avionics anti collision software). They then use the SMV model checker to verify that their system accomplishes its tasks correctly. They also present a number of ways to reduce the state space explosion problem to acceptable levels. Their approach is one of symbolic model checking. Cho & al. [Cho99] propose the use of APromela, an extension of the Promela language designed to abstract actors, to apply model checking to concurrent systems using the SPIN model checker. Their approach proposes to translate APromela notations to Promela instead of building an entirely new tool. Lam & al. [Lam04, Lam05] propose to use the NuSMV model checker to perform model checking on concurrent systems formalized using p-Calculus. p-Calculus is a process algebra specifically designed to specify concurrent systems in which processes communicate through channels. The authors propose to translate p-Calculus notations, based on the Labelled Transition System (LTS), to Kripke structures notations on which is based the NuSMV input language. However interesting, this approach only focuses on the individual behavior of objects by verifying only formalized state transition diagrams. All these approaches mainly focus on verifying one or two aspects of object-oriented systems using model checking, namely the structural aspects and / or the individual behavior of objects. Only the approach proposed by Merz & al. [Merz01] considered the collective behavior of objects while leaving out the structural aspects. We present, in this paper, a more global approach that allows the generation of a Maude formal specification integrating both static and dynamic (individual and collective) features of object-oriented systems. We use UML class diagrams to represent static features of an object-oriented system, and state and communication diagrams (respectively individual and collective behavior) to represent its dynamic features. We also focus on some aspects of concurrent object-oriented systems (external concurrency). The formal and object-oriented language Maude, based on rewriting logic, supports the formal specification and programming of concurrent systems [Meseguer92, Clavel99, McCombs03, Eker02, Meseguer03, Clavel05]. It also offers a model checking environment. Maude is a multi paradigm language [Meseguer03, Clavel05] that supports the semantics of concurrency (intra and inter-objects). Furthermore, the Maude language is supported by a tool, which allows validating the generated formal descriptions through simulation, as we will illustrate it in the next sections. Maude also integrates a model checker supporting the verification of Linear Temporal Logic (LTL) properties [Eker02, Meseguer03, Clavel05]. The Maude environment is still not very used. We wished to explore its possibilities in both formal specification and model checking aspects of concurrent UML diagrams. 3 UML DIAGRAMSClass DiagramUML class diagrams express the static structure of a system in terms of classes and relationships between classes. Classes are essentially organized through aggregation, inheritance or association relationships [Muller00, OMG05]. State DiagramUML state diagrams [Muller00, OMG05] describe, using finite state machines, the life cycle of objects. Different types of event are defined by UML. We will focus only on the events of the "Call" type. State Diagrams can also be concurrent in nature [Börger00, Börger03, Schmidt99]. In fact, a composite state can have several orthogonal regions, each active at the same time that the composite state is active. This form of State Diagram models the internal concurrency of a class and models how several subtasks can be executed concurrently in the execution of a more global task accomplished by a class. Each orthogonal region of a composite state is seperated by a dashed line. Entry in each of these regions is done through the use of an initial state or through a fork structure (which then in turn requires a join structure when leaving the composite state). Communication DiagramUML Communication diagrams [OMG05], known as Collaboration diagrams in previous versions of UML [Booch98, Muller00] describe how a set of objects collaborate to accomplish a specific task. They emphasize the dynamic interactions between those objects (message exchanges) as well as their synchronization. A message sent can be so in two different manners: synchronous or asynchronous. The messages sent between two classes can be sequential (with messages of the same level having a sequence number incremented, for example 1, 2, 3, ), concurrent (two concurrent messages will have the same sequence number, differentiated only by an added name, for example 1a and 1b), or they can be both at the same time. The concept of synchronization between messages is accomplished using the "/" symbol. A synchronization point is used to note the necessity of the completion of a particular message before the execution of another can begin, for example. 4 REWRITING LOGIC AND MAUDERewriting LogicRewriting logic, having a sound and complete semantics, was introduced by Meseguer [Meseguer92]. It allows describing concurrent systems [Meseguer03, McCombs03, Eker02, Clavel05]. This logic unifies all the formal models that express concurrency [Meseguer90]. The rewriting rules are of the form R : [t] MaudeMaude is a specification and programming language based on rewriting logic [Meseguer92, Clavel99, Clavel05, McCombs03]. Three types of modules are defined in Maude. Functional modules allow defining data types and their functions. System modules allow defining the dynamic behavior of a system. This type of module augments the functional modules by introducing rewriting rules. Finally, object-oriented modules, which can be reduced to system modules, offer a more appropriate syntax to describe the basic entities of the object paradigm. Subsection Model checking and Maude of Section 7 will deal more specifically on how Maude can be used for model checking. Fig. 1 shows a small Maude program. Fig. 1. Short program in Maude The example shown in Fig. 1 gives the definition of three types: Configuration, Object and Msg (those two last being subtypes of Configuration). In the case where there is no floating messages or live objects, the global configuration of the system is empty. The construction of a new configuration, in terms of other configurations, is done with the operation given on line 7. This operation satisfies the structural laws of associability and commutability and possesses a neutral element called null. 5 TRANSLATING UML DIAGRAMS INTO MAUDEThe adopted translation process consists of systematically deriving a Maude formal specification from an analysis of the UML class, state and communication diagrams. Fig. 2 presents the steps of the translation process we elaborated in [Mokhati06]. The diagrams go through a first verification step to make sure, for example, that each message sent to a destination object in the communication diagram exists in the state diagram and that it is accessible. During the translation process of the considered UML diagrams, several Maude modules are generated. Fig. 3 shows those modules. Please note that modules in bold are object-oriented modules, while all others are system modules. As for programming purposes, all object-oriented notations will be reduced to its system form.
Fig. 2. Overview of the Translation Process
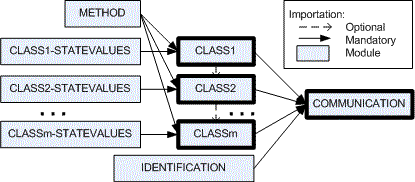
Fig. 3. Generated modules The functional module METHOD (see Fig. 4) contains all the types used to describe a method. Types Parameter and ParameterList are generic. They describe the type of parameters a method uses. Furthermore, ResultType and Void describe the type of the result returned by the method. ResultType is generic, and Void is a particular case of ResultType. The operation (_,_) is a constructor for the parameter list of a function.
Fig. 4. The METHOD module We associate to each state diagram a functional module for which the name is the concatenation of the class' name and the string STATEVALUES'. The functional module IDENTIFICATION is generated to describe the identification mechanism of the objects of the communication diagram. For each class of the class diagram, we associate an object-oriented module bearing the same name as the class, while adopting a generic form for the classes (Fig. 5). In the case where one of such a class is in relation to other classes in the class diagram, the module associated to it must import all the other modules associated to those classes. The class is declared in a module with an attribute called State and for which its type is declared in the corresponding functional module. This attribute is automatically added to all classes to model its objects' state. It has for objective to explicitely note the objects' state. In the case of an aggregation class, an identification list of all the aggregated classes must also be present as attribute to the class. The generic form of classes also shows an open attribute list and a regional states list, which is explained further on.
Fig. 5. Generic form adopted for the classes, with optional regional substates for concurrent composite states, an optional component list and an opened list of attributes The modules in which are declared the classes also contain the declaration of the class' methods. Each of the functions are declared using the generic form shown in Fig. 6. ParameterList and ResultType were introduced in the METHOD module (Fig. 4).
Fig. 6. Form adopted for the methods The translation process was mainly developed for traditional sequential programs. However, concurrent systems require slight modifications to the adopted process. Since Concurrent Object-Oriented Systems (COOS) are based on objects, the basic structure remains the same and so does the general translation process. The main element in which more attention is required when translating external concurrency is the fact that two (ore more) objects are active (executing) at the same time. Therefore, rewriting rules must be produced accordingly in the COMMUNICATION module. See below for further details on this module. As for internal concurrency, the best option is to model the class with more State attributes, one for each of the orthogonal regions of its concurrent composite state. For example, a class that has a concurrent composite state with 2 orthogonal regions, aside from the main State attribute described above, there will be two more. This also means that the STATEVALUES' module for that class will also define two new sorts with their respective values, in the same manner defined earlier. We also introduce an Inactive value for those "regional" substates for when the object is not in its concurrent composite state. All the while an orthogonal region is active within a concurrent composite state, the object remains in this composite state, and only the "regional" states' values vary. When all the orthogonal regions have completed their execution, the object can now leave its concurrent composite state. Then, all "regional" states are put in their Inactive state. The object-oriented module COMMUNICATION is the principal one generated by our approach. It imports all the other modules. In it, we extend all the other object-oriented modules by describing the behavior of the different objects involved in the communication diagram using rewriting rules. Each message exchanged between two objects of the communication diagram is translated in the form of a ComingMsg (Fig. 7).
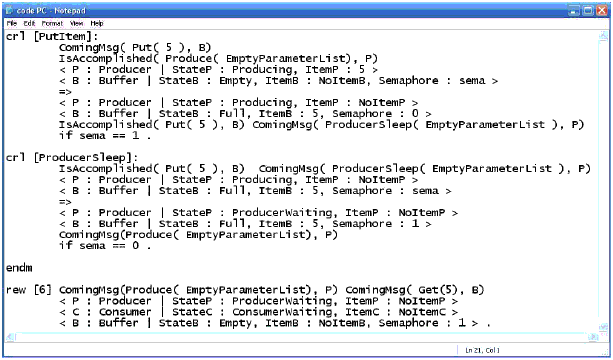
Fig. 7. Form adopted for the messages With this message, we specify two things. On the first hand, we identify the destination object ( Receiver ) and, on the other hand, the result type of the operation to be executed. In fact, each sending of a message in the communication diagram corresponds to a Call Event, launching a transition in the state diagram of the destination object. This transition is described in this module whether by an unconditional rewriting rule in the case where the sending of the message is not linked to a condition or by a conditional rewriting rule otherwise. To implement the concept of Synchronization Point of the messages sent within a communication diagram, we introduce a new message called IsAccomplished (see Fig. 8). The rewriting rule that implements a transition corresponding to the sending of a message on which depends other messages must generate a number of IsAccomplished messages equal to the number of messages to be sent. To better illustrate the use of the IsAccomplished synchronization message, consider the ProducerSleep message of Fig. 11, where it is required that message Put be completed for it to be executed.
Fig. 8. Form of the synchronisation message The IsAccomplished message does not represent a message sent between two objects in the communication diagram. It must be interpreted as an indication that the sending of the message is terminated. As mentionned previously, we focused in this paper on external concurrecy. The considered example will not show any internal concurrency. However, internal concurrency has been considered in our work in others case studies (not adressed in this paper). 6 CASE STUDYPresentationTo illustrate our approach, we present a simple, yet concrete case study. In the present section, only the translation of the example's UML models to Maude formal specifications is introduced. The formal verification of the models using Model Checking techniques is addressed in the next section.
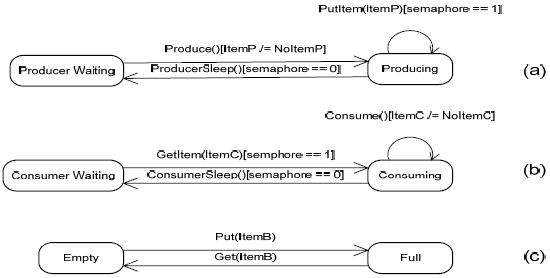
Fig. 9. Class Diagram of the system The example we chose to illustrate our approach is a simple concurrent object-oriented system. It is based on the classic Producer Consumer problem. Our example is an adaptation between the examples presented in [Gomaa00] and [Meseguer03]. Fig. 9 presents the UML Class Diagram associated to this system. Our system is then composed of 3 classes. The first class, called Producer, is designed to have objects generating integer elements (the Produce function) as information to transmit (through the PutItem function). The class has also a ProducerSleep method that puts an object into a suspended state while the memory buffer is unavailable to receive new information. The Consumer class is designed to have objects that will be getting information from a memory buffer through its GetItem function and use that information in some manner with the Consume function. This class also possesses a ConsumerSleep function that, similarly to class Producer, puts the objects of that class into a suspended mode while the buffer has no new information to transmit. The last class, Buffer, is the memory buffer of the system. It has an ItemB attribute, which is the memory buffer in itself, and is of size 1. Therefore, the Buffer can contain only one integer information at a given time. Functions Put and Get are used respectively to collect information coming from a Producer object, and transmit that information to a Consumer object. The public attribute Semaphore will be used for coordination purposes between the Consumer and the Producer of the system. It will take only values 0 or 1, interpreted as follows: when Semaphore == 1, the memory buffer is free and can be used by either a Producer object to put a new element, or by a Consumer object to get an existing element. When Semaphore == 0, the memory buffer is already used by an object and is locked, preventing any other object the possibility of using the shared resource. Figure 10 presents the corresponding State-Transition Diagrams. Diagram (10.a) is associated to the Producer class, where the transition associated to a procedure call of the PutItem function is guarded by a condition on the Buffer object's Semaphore attribute. The GetItem procedure call transition of Diagram (10.b) associated to a Consumer object is similar. Finally, diagram (10.c) is associated to a Buffer object. The system we consider in our example present concurrent aspects since objects of classes Producer and Consumer can attempt to access the Buffer object at the same time. Each object of those two classes will then have its own process within the system and are considered as Active Objects.
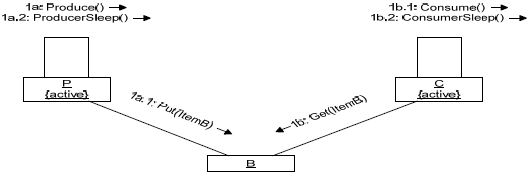
Fig. 10. State-Transition Diagrams for classes (a) Producer, (b) Consumer and (c) Buffer In the communication diagram of Fig. 11, we observe a Producer object attempting to write information in a Buffer object's memory and at the same time a Consumer object attempts to read the information contained in the Buffer object. Since the PutItem and GetItem functions of classes Producer and Consumer respectively are guarded with the use of Buffer 's Semaphore attribute, simultaneous reading and writing on the shared resource Buffer is not allowed.
Fig. 11. Communication Diagram of the System Application of the Translation ProcessIn this section, we illustrate the application of the translation process (Section 5) to the example described above. We focus here on the translation to Maude notations. Three Maude functional modules are introduced to describe the state values of each class present in the system. Those three modules are named PRODUCER-STATEVALUES, CONSUMER-STATEVALUES and BUFFER-STATEVALUES, respectively for classes Producer, Consumer and Buffer. For space limitation reasons, only one of those modules is shown here, namely PRODUCER-STATEVALUES (Fig. 12).
Fig. 12. Module PRODUCER-STATEVALUES A module IDENTIFICATION (Fig. 13) imports the predefined CONFIGURATION module. This module contains the definition of types Poid, Coid and Boid which describe the identification mechanism of the objects P, C and B, instance of classes Producer, Consumer and Buffer respectively.
Fig. 13. Module IDENTIFICATION Knowing that the system we study has 3 classes (Producer, Consumer and Buffer), three object-oriented modules are generated by our approach, respectively named PRODUCER, CONSUMER and BUFFER, which will introduce each of the classes and their respective methods. For space limitation reasons, only one of those modules is given, namely the object-oriented module PRODUCER in Fig. 14. The Producer class is defined with 2 attributes, StateP will contain information about the current state of the object (for which the possible values are given in module PRODUCER-STATEVALUES of Fig. 12), and an attribute ItemP that will contain the produced item that the Producer object will transmit to the Buffer. The class has 3 methods. The first is named Produce and is the method that will create an item of information destined to be transmitted to the Buffer. The second method is called PutItem and is the actual method that will transmit the information to the Buffer object by a method call. The last method is called ProducerSleep, and has for objective to put the Producer object into a suspended mode when the transmission to the Buffer object is completed. Finally, the NoItemP operator is actually a new possible value for integer variables, and will represent the fact that the ItemP attribute of a Producer object contains no value.
Fig. 14. Module PRODUCER Module COMMUNICATION is the primary module generated. It contains rewriting rules modeling the behavior of the system concerning the realization of a specific task given in the communication diagram of Fig. 11. Specifically, the task consists on a concurrent get and put access to a memory Buffer by two active objects. Fig. 15 shows part of the COMMUNICATION module. As specified earlier, the module imports all the other modules defined namely IDENTIFICATION, PRODUCER, CONSUMER and BUFFER.
Fig. 15. Part of the COMMUNICATION module The part of the module shown in Fig. 15 concerns more closely the behavior of objects of the Producer class. Maude being particularly developed for the modeling of concurrent systems (as stated in Section 4), it is therefore appropriate for the modeling of active objects like we have in the system we consider. Two rewriting rules are shown in Fig. 15. Rule ' ProduceItem ' shows the behavior of such an object when it receives a Produce ' message to start producing integer element to transmit to the Buffer object. This method then generates an integer element and places it in the ItemP attribute. For the execution to take place, the ItemP attribute must not already contain an element (condition of the translation rule). A IsAccomplished message is generated to allow the execution of the second rewriting rule. The second rule, PutItem ' is actually intended to model the execution of the PutItem method. This method uses the Put function of a Buffer object to transmit the integer element to the shared memory, while insuring this resource is not already used by another object (guard condition). A IsAccomplished message is also generated so that the third rule can be executed ( ProducerSleep '), effectively putting the Producer object into its ProducerWaiting state. The Producer object then waits until the shared memory of Buffer is once again available to receive new information. See Fig. 11 for further information. Validation of the Generated DescriptionConcerning the verification of the developed models, rewriting logic and Maude are very versatile with simulations, since it allows the selection of a personalized initial configuration from which to start the simulation. It is very useful when attempting to verify part of a system while not compromising the rest of it. The first verification we attempt is started from the initial configuration shown in Fig. 16. This configuration is composed of two objects, P and B of classes Producer and Buffer respectively, both containing no item. We also have a Produce message sent to P. The results of this verification are given in Fig. 17.
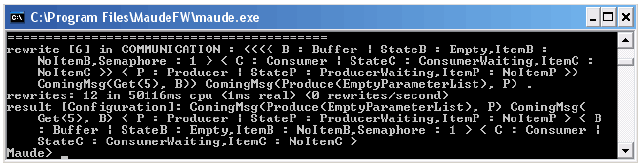
Fig. 16. Initial configuration The results (Fig. 17) can be interpreted as follows. Following the execution of message Produce, object P has produced an integer element, here 5, and transmitted it to the shared memory of a Buffer object. P is then in its ProducerWaiting state and awaits the next time B is available and in its Empty state. Finding a new ComingMsg to produce a new item is correct knowing that the classic Producer Consumer problem is a perpetual process that goes on until stopped.
Fig. 17. Result of the unlimited rewriting of the initial configuration of Fig. 16 We will now attempt to verify the behavior of a Consumer object. To perform this verificaiton, the initial configuration of Fig. 18 is used, and the results are given in Fig. 19. This initial configuration is composed of a C object and a ComingMsg to try and get an element available from the Buffer. The initial configuration also shows a B object of the Buffer class, already contaniting an element (here, 5). Its StateB attribute is set to Full, and Semaphore to 1 to signify B is not currently used by another thread.
Fig. 18. An initial configuration The results of the rewriting of Fig. 18's initial configuration can be interjpreted as follows. C, after getting and consuming an element of information from Buffer is in its ConsumerWaiting state, awaiting a new integer information available in the Buffer. B is now Empty, since the information it contained was taken by C, and the system generates a new ComingMsg destined to C to try and get new information from the Buffer, conforming to the perpetual execution untill stopped idea. Having verified the behavior of objects of the Producer and Consumer classes respectively, we can now proceed on to the verificaiton of the behavior of the entire system altogether.
Fig. 19. Result of the unlimited rewriting of the initial configuration of Fig. 18
Fig. 20. Part of the developed code Fig. 20 shows part of the Maude code we developed. It shows, on the first hand, rewriting rules PutItem ' and ProducerSleep ' that model part of the behavior of the Producer objects and, on the second hand, one rewriting command issued to the Maude environment. This simulation is started from an initial configuration where we have three different objects, P, C and B, respectively of classes Producer, Consumer and Buffer, in their initial states, as well as incoming messages Produce and Get as shown in the communication diagram of Fig. 11. The number of rewriting steps is limited to 6 since the system is modelled as an infinite loop, and is therefore not terminating.
Fig. 21. Results of the rewriting of Fig. 20 Fig. 21 shows the results of this rewriting command. The limited rewriting grants us the possibility of visualizing that the system behaves properly. As we can see, the system eventually returns to its actual initial state, which is exactly what it should do according to the classic Producer Consumer problem. 7 APPLYING MODEL CHECKINGIn our opinion, the verification of the collective behavior of a group of objects that are collaborating to accomplish a specific task begins with the verification of the individual behavior of the objects. We propose, in what follows, an incremental process for the definition and verification of properties to be verified within our system. The properties we propose are defined in LTL. The next subsection exposes the generic process to use Maude's model checker. We then propose 4 properties relevant to the individual behavior of objects P, C and B, instances of classes Producer, Consumer and Buffer respectively. The following subsection proposes 3 properties related to the collective behavior of those same objects. The final subsection describes the adopted process to verify the proposed properties. Model Checking and MaudeAs was illustrated in Section 6, an object-oriented system can be described with relative ease using the Maude language. With the help of a single rewriting rule, we can express many things: the consumption of floating messages, the sending of new messages, the destruction of objects, the creation of new objects, as well as state changes. However, Maude offers another important tool in the verification of a system: it has an integrated model checker that verifies LTL properties in the system under development [Clavel05, Eker02, MacColl99, Meseguer90, Meseguer92, Meseguer03]. However, using that model checker implies the use of a technique, which we introduce briefly in this subsection. We then use it to perform more advanced verifications on our example. Maude supports model checking with LTL properties mainly for its simplicity and the well defined decision procedures it offers [Clavel05, McCombs03]. Fig. 22 illustrates the defined LTL operators. Other operators exist, but can be derived from those primary operators.
Fig. 22. A module in Maude implementing the operators of LTL logic For the definition of LTL properties, we need an operator to determine the result, True or False, of a property in a certain system state. For that, the |= operator is introduced in the predefined SATISFACTION module (Fig. 23).
Fig. 23. The SATISFACTION module It is then possible to define diverse system properties in a new module that imports both the SATISFACTION module and the module or modules defining the system to be studied. Fig. 24 shows the M-PREDS module, in which predicates about the system are defined. Those predicates will be used to later define LTL properties about the system. Also note that M symbolizes a module in which the studied system is modelled.
Fig. 24. The M-PREDS module The next step in the model checking process of Maude consists on the definition of a final module called M-CHECK in which all the elements are bound together for the verification. We also introduce all the initial configurations used in the verification process in this module. Figure 25 shows the M-CHECK module.
Fig. 25. The M-CHECK module The final step consists on launching the verification calls into the Maude system using the modelCheck function of module MODEL-CHECKER. (Fig. 26).
Fig. 26. The MODEL-CHECKER module To give a small overview of a typical model checking call using Maude, Fig. 27 shows the generic form used to launch a verification. In this call, initial_state represents an initial configuration of the system where the verification should start, and LTL_property expresses a desirable or non desirable requirement that the system should verify. This LTL property is the one that is getting verified with this call.
Fig. 27. A typical model checking call Properties Related to the Individual Behavior of ObjectsIn this section, we propose 4 properties related to the individual behavior of objects P and C. Properties 1 and 2 concern the behavior of P, and properties 3 and 4 are relevant to the behavior of C.
Properties Related to the Collective BehaviorIn the previous section, we introduced properties of the individual behavior of objects P and C. We now introduce 3 other properties to verify the collective behavior of those same objects.
Fig. 27 presents a part of the COMMUNICATION-PREDICATES module, in which we define the predicates relative to the Producer - Consumer system we are studying. We define, in this module, the necessary operators that we used in the definition of the properties that we wish to verify. We limit the shown predicates to the ones relative to the class Producer. Lines 1 and 2 show respectively the predicate associated to the Producing state of class Producer and the one associated to the ProducerSleep state. The predicates relevant to the other class are omitted since they are very similar to the ones presented here.
Fig. 27. The COMMUNICATION-PREDICATES module Properties VerificationAs mentioned previously, the Maude environment has an integrated model checker, in the form of the modelCheck function of module MODEL-CHECKER. Fig. 28 shows the module COMMUNICATION-CHECK in which is defined the initial configuration used: initial1. It is the same initial configuration used for the simulation of the entire system in Subsection Validation of the Generated Descriptions of Section 6.
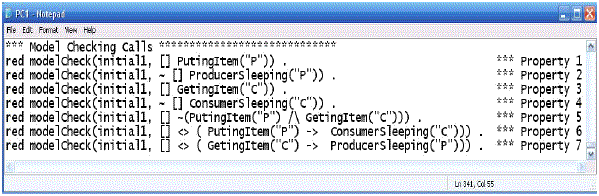
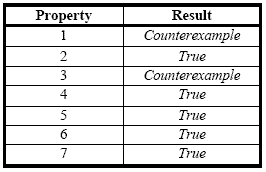
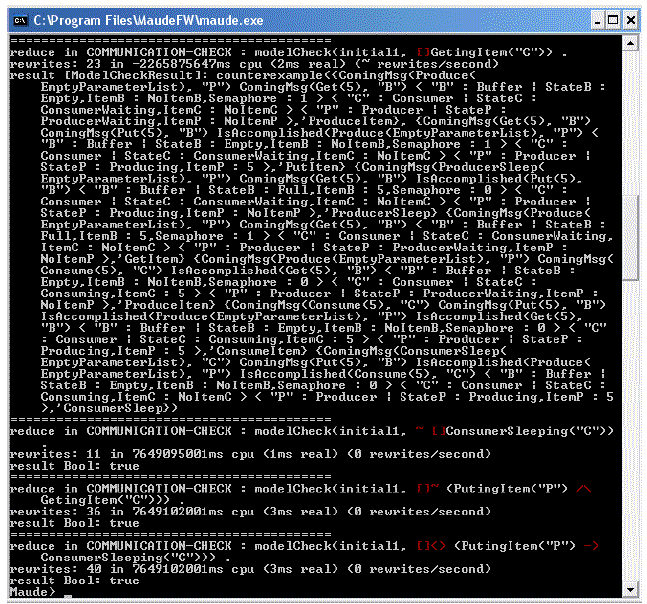
Fig. 28. The COMMUNICATION-CHECK module describing the initial state used All the necessary elements to proceed to the verification are now defined. Fig. 29 shows the calls to the modelCheck function of Maude, seven in all, one for each of the properties that were defined previously. Fig. 30 shows part of the results obtained with Maude. Maude evaluated all the properties in less than a second. Table 1 shows a summary of the results of the evaluation of the 7 properties. They are as follows: on the 7 properties evaluated, 5 have a positive result ( True ) meaning that those properties are verified within our system. Two of the properties, however, show a Counterexample result, meaning that they were not verified, and the Counterexample shows the exact path the Maude modelCheck algorithm took to reach the error state. The two properties showing a negative result are relevant to the individual behavior of objects, one for Producer and one for Consumer.
Fig. 29. Model Checking calls
Table 1 : Results of the evaluation of the properties The results can be interpreted as follows. Let us firstly consider the results relevant to the individual behavior of objects. For object P of the Producer class, for which 2 properties were defined to verify its behavior (properties 1 and 2), the results confirm that the object behaves correctly. In fact, Property 1, aimed at verifying if the object was always in its critical section of transmitting information to the Buffer, the result obtained is a Counterexample. However, obtaining a negative result actually means the system does not allow the Producer to eternally be in its critical section, which is the intended behavior. The second property, defined to verify the possibility of the Producer not being in its ProducerSleeping state forever returned a positive result ( True ). This property being verified means the system does not allow this situation. The properties concerning the behavior of the Consumer are very similar in nature to the ones relevant to the Producer. Properties 3 and 4 are then analogous to Properties 1 and 2. Property 3 attempted to verify if the system allowed the Consumer to be in its critical section (getting information from the Buffer ) forever. The result was a Counterexample, meaning that such a situation was not possible. Property 4, on its part, attempted to verify that the system did not allow the Consumer to be locked in its ConsumerWaiting state. Because this property was defined using the combination ~ [] combination of temporal operators and that the result was True, this characteristic is not allowed by the system. Finally, the three last properties, relevant to the collective behavior of objects P, C and B, were all evaluated to True, meaning they all have been verified. Property 5 was intended to verify if the system allowed for P and C to be in their respective critical section at the same time. The positive result knowing that the ~ temporal operator was used proves that this situation is impossible within our system (mutual exclusion is then satisfied). Properties 6 and 7 were used to insure that it is infinitely often true that while one thread is in its critical section, the other is not. Property 6 verified that if a Producer object is in active mode, the Consumer object is sleeping, while Property 7 verified the counterpart (namely if a Consumer object is in active mode, the Producer object is sleeping). Those two properties were both evaluated to True.
Fig. 30. Part of the results of the Model Checking calls of Fig. 29 8 CONCLUSIONS AND FUTURE WORKThe translation of UML diagrams in formal languages has been addressed in numerous papers. Several tools helping the translation process have been developed. However, the majority of those approaches did not consider the collective behavior of objects. In this paper, we proposed a generic approach that allows the translation of static aspects (described by UML class diagram) and dynamic aspects (described by UML state and communication diagrams) of object-oriented systems into a Maude formal specification. More particularly, we applied the translation process we developed in [Mokhati06] to a concurrent object-oriented system. Such a specification integrates both static and dynamic features of the described system. However, our approach is limited to basic state and communication diagrams, modelling the most common features. The Maude language is supported by a tool, which allowed us to validate the generated code by simulation. Moreover, Maude offers a model checker in its environment, which uses Linear Temporal Logic (LTL) to verify properties among the models developed [Eker02, Meseguer03, Clavel05]. We defined some LTL properties about our system and used Maude's model checker to verify them. It is to be noted that the example used is small and simple and is aimded to test the notations we developed. The properties we defined included inherent problems known to concurrent systems, such as deadlocks. Among future directions to this work, we plan on testing the approach on larger scale examples and integrating other UML diagrams.REFERENCES[Araujo00] J. Araujo and A. Moreira. "Specifying the Behavior of UML Collaborations Using Object-Z". Departamento de Infomatica, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa, Portugal, 2000. [Astesiano98] E. Astesiano. "UML as Heterogeneous Multiview Notation. Strategie for a Formal Foundation". In Proceedings of OOPSLA'98 Workshop on Formalizing UML. Why? How?, L. Andrade, A. Moreira, A. deshpande, and S. Kent, editors,, Canada, 1998. [Barnett04] M. Barnett, R. DeLine, M. Fahndrich, K. Rustan, M. Leino, and W. Schulte. "Verification of object-oriented programs with invariants", In Journal of Object Technology, vol. 3, no. 6, June 2004, Special issue: ECOOP 2003 workshop on FTfJP, pp. 2756, http://www.jot.fm/issues/issue_2004_06/article2/ [Booch98] G. Booch, J. Rumbaugh et I. Jacobson. The Unified Modeling Language User Guide, Addition-Wesley, Object Technology Series, 1998. [Börger00] E. Börger, A. Cavarra, and E. Riccobene. "Modeling the Dynamics of UML State Machines". In ASM '00 : Proceedings of the International Workshop on Abstract State Machines, Theory and Applications, pages 223241, London, UK, 2000. Springer-Verlag. [Börger03] E. Börger, A. Cavarra, and E. Riccobene. "The Meaning of Concurrent States in UML State Diagrams". Presentation Slides for SAC 2003. [Bowen03] J. Bowen. Formal Specification and Documentation Using Z: A Case Study Approach, 2003. [Bruel00] J.M. Bruel, J. Lilius, A. Moreira, and B. Robert."Defining Precise Semantics for UML". In ECOOP'2000 Workshop Reader, Cannes, France, number 1964 in Lecture Notes in Computer Science. Springer-Verlag, November 2000. [Canals03] Canals et al. "How You Could Use NEPTUNE in the Modelling Process". In Journal of Object Technology, vol. 2 num. 1, pages 6983, 2003, http://www.jot.fm/issues/issue_2003_01/article1 [Chan98a] W. Chan, et al. "Model checking large software specifications". In IEEE TSE, vol. 24, num. 7, pp 498520, July 1998. [Chan98b] W. Chan et al. "Improving efficiency of symbolic model checking for state-based system Requirements". In ISSTA 98 : Proceedings of the ACM SIGSOFT International Symposium on Software Testing and Analysis. Michal Young, editor,, pp 102112, Clearwater Beach, USA, March 1998. [Cho99] S. M. Cho, D. Hwan Bae, S. Deok Cha, Y. Gon Kim, B. Kyu Yoo, and S. Taek Kim. "Applying model checking to concurrent object-oriented software". In ISADS '99: Proceedings of the The Fourth International Symposium on Autonomous Decentralized Systems, page 380, Washington, DC, USA, 1999. IEEE Computer Society. [Clavel99] M. Clavel and al. "Maude: Specification and Programming in Rewriting Logic". Internal report, SRI International, 1999. [Clavel05] M. Clavel, F. Durán, S. Eker, P. Lincoln, N. Martí-Oliet, J. Mesenguer, and C. Talcott. Maude Manual (Version 2.1.1), April 2005. [Dong00] Dong J. S. "Formal Specification and Design Techniques". Lecture Notes, 2000. [Eker02] S. Eker, J. Meseguer, A. Sridharanarayanan. "The Maude LTL Model Checker". Elsevier Science B. V., 2002, 27 pages. URL: http://www.elsevier.nl/locate/entcs /volume71.html [Favre05] L. Favre: "Foundations for MDA-based Forward Engineering", in Journal of Object Technology, vol. 4, no. 1, January-February 2005, pp. 129-153. http://www.jot.fm/issues/issue_2005_01/article4 / [Funes02] A. Funes and C. George. "Formal Foundations in RSL for UML Class Diagrams". Technical Report 253, UNU/IIST, May 2002. [Gallardo02] M. del Mar Gallardo, P. Merino, and E. Pimentel. "Debugging UML designs with model checking". In Journal of Object Technology, Vol. 1(No. 2): pages 101117, 2002. http://www.jot.fm/issues/issue_2002_07/article1/ [Garcia02] E. García-Roselló et al: "Design Principles for Highly Reusable Concurrent Object-Oriented Systems", in Journal of Object Technology, vol. 1, no. 1, May -June 2002, pages 107-123, http://www.jot.fm/issues/issue_2002_05/article3/ [Gomaa00] H. Gomaa. Designing Concurrent, Distributed, and Real-Time Applications with UML. Addison-Wesley Longman Publishing Co., Inc., Boston, MA, USA, 2000. [Jean-Pierre05] S.V. Jean-Pierre, H. Malgouyres et G. Motet. "Identification de règles de cohérence d'UML 2.0", Journée SEE "Systèmes Informatiques de Confiance" on the theme of " Vérification de la cohérence de modèles UML ", France (Mars 2005). [Ledang03] H. Ledang. J. Souquières et S. Charles. "ArgoUML+B : un Outil de Transformation Systématique de Spécifications UML en B". In Actes de la conférence AFADL '03, INRIA, pages 15-17, Rennes, France, Janvier 2003. [MacColl99] I. MacColl and D. Carrin gt on. "Specifying Interactive Systems in Object-Z and CSP". Software Verification Center, Department of Computer Science & Electrical Engineering, University of Queensland, Australia, 1999. [McCombs03] T. McCombs. "Maude 2.0 Primer, Version 1.0". Internal report, SRI International, 2003. [Meng04] S. Meng, Z. Naixiao and B. K. Aichernig. "The Formal Foundations in RSL for UML Statechart Diagrams". Technical Report 299, UNU/IIST, July 2004. [Merz00] S. Merz. "Model checking : A Tutorial Overview". In MOVEP, volume 2067 of Lecture notes in Computer Science Franck Cassez, Claude Jard, Brigitte Rozoy, and Mark Dermot Ryan, editors, pages 338. Springer, 2000. [Merz01] S. Merz, T. Schäfer and A. Knapp. "Model checking UML state machines and collaborations". Electronic Notes in Theoretical Computer Science, volume 55 (no. 3), 13 pages, 2001. [Lam04] V. S. W. Lam and J. A. Padget. "Symbolic Model Checking of UML Statechart Diagrams With an Integrated Approach". In ECBS, pages 337347, 2004. [Lam05] V. S. W. Lam and J. A. Padget. "An Integrated Environment for Communicating UML Statechart Diagrams". IEEE Computer Society, 2005. [Meseguer90] J. Meseguer. "Rewriting as a unified model of concurrency". In Proceedings of the Concur'90 Conference, Amsterdam, Pages 384-400, Springer LNCS Vol. 458, 1990. [Meseguer92] J. Meseguer. "A Logical Theory of Concurrent Objects and its Realization in the Maude Language". In Research Directions in Object-Based Concurrency, G. Agha, P. Wegner, and A. Yonezawa, Editors. MIT Press, 1992. [Meseguer03] J. Meseguer. "Software Specification and Verification in Rewriting Logic". Unpublished work. Computer Science Department, University of Illinois at Urbana-Champaign, 2003. [Mokhati06] F. Mokhati, M. Badri and P. Gagnon. "Translating UML Diagrams into Maude Formal Specification: A Systematic Approach". In SEKE'06: Proceedings of the 18th International Conference of Software Engineering and Knowledge Engineering, San Francisco, 2006. [Muller00] P.A. Muller et N. Gaertner. Modélisation objet avec UML, Deuxième Edition, Paris, 2000. [OMG05] Object Modeling Group. "Unified Modeling Language Specification", version 2.0, July 2005. [Paige02] R.F. Paige, L. Kaminskaya, J.S. Ostroff and J. Lancaric. "BON-CASE: an Extensible CASE Tool for Formal Specification and Reasoning". In Journal of Object Technology, volume 1 no. 3, pages 65-87, August 2002. http://www.jot.fm/issues/issue_2002_08/article5/ [Paige04] R.F. Paige and P.J. Brooke. "Integrating BON and Object-Z". in Journal of Object Technology Vol. 3, No. 3, pages 121-141, March-April 2004. http://www.jot.fm/issues/issue_2004_03/article3/ [Reggio04] G. Reggio and R. Wieringa. "Thirty one Problems in the Semantics of UML 1.3 Dynamics". In OOPSLA'99 Workshop "Rigorous Modeling an Analysis of the UML Challenges and Limitations", 1999. [Schmidt99] J. W. Schmidt and F. Matthes. "State Diagrams". Presentation Slides, 1999. [Snook04] C. Snook, and M. Butler. "U2B - A tool for translating UML-B models into B", In UML-B Specification for Proven Embedded Systems Design, Springer (In press), 2004. [Taibi03] T. Taibi, D. Check Ling Ngo. "Formal Specification of Design Patterns A Balanced Approach", in Journal of Object Technology, vol. 2, no. 4, 2003, pp. 127-140. URL: http://www.jot.fm/issues/issue_2003_07/article4/ [Tigris02] ArgoUML Tigris Organisation. (2002): ArgoUML User Manual 2002, URL: http://argouml.tigris.org/ documentation /defaulthtml/manual/. [Wahl03] Thomas Wahl. "(Yet Another) Introduction to Model Checking". Presentation Slides, Spring 2003. [Wegner90] Peter Wegner. "Concepts and Paradigms of Object-Oriented Programming". In SIGPLAN OOPS Mess., Vol. 1(No. 1) : pages 787, 1990. About the authors
Cite this article as follows: Patrice Gagnon, Farid Mokhati, Mourad Badri: "Applying Model Checking to Concurrent UML Models", in Journal of Object Technology, vol. 7, no. 1, January-February 2008, pp. 59-84, http://www.jot.fm/issues/issue_2008_01/article1/ |
|||||||||||||