AbstractState machines can be used to specify the behaviour of objects in a system by describing the relationships between the states of the object and its ability to respond to events presented to it. Suitable choice of semantics for state machines allow multiple machines to be composed in the description of a single object. We describe an extension to this approach whereby different machines in the composition of a single object have different semantic types covering necessary behaviour, encouraged behaviour and discouraged behaviour. This provides expressive power to model the way software interacts with the domain to encourage or discourage events. 1 INTRODUCTIONBackgroundThis paper describes a technique for modelling object behaviour that enables different types of behaviour rule to be composed in the description of an object, whereby the behaviour of an object is governed by rules that represent not only what is possible but also what is allowed or desired. The ideas presented in this paper have emerged from experience over 15 years in building and using tools that support the behavioural design of transactional business systems. Our particular interest has been to provide tools that allow behavioural models to be executed and tested early in the development lifecycle, so that the risk that severe behavioural problems are found at late stages of testing, when rectification can be very expensive, is significantly reduced. The executable models can be viewed as a form of prototype, and the testing and exploration of such prototypes provides a vehicle for users and other stakeholders to engage in and contribute to the modelling process, even if they have no understanding of the notations and concepts used to build the model. Domain of InterestThe systems we are concerned with are those normally termed "transactional business systems". This class includes such familiar applications as accounting, order processing, workflow, stock control, etc. For the purposes of this paper, we make the following assumptions about the form and behaviour of such a system:
Here an "event" (properly, an "event instance" 1) is the data representation of an occurrence of interest in the real world domain. Examples of such real world occurrences are "Customer Fred places an order for 100 widgets to be delivered on 12th August " or "Policy holder Jim makes a claim for £250 against policy number P1234". These occurrences are considered to be atomic and instantaneous in the domain. An event represents such an occurrence as a set of data attributes or parameters. Every event is an instance of an event-type and the type of an event determines its metadata (or attribute schema), this being the set of data attributes that completely define an instance of the event-type. In a banking system, for instance, an event-type might be "Withdraw" with metadata (Account Id, Date and Time, Amount). The passage of time is also modelled as events, such as "end of day". This approach to modelling events is identical to that used in other event based modelling approaches, for instance Jackson System Development [Jac83] and Syntropy [Coo94]. The set of assumptions given above are over-restrictive for "real" systems, as timing issues are completely ignored. In particular, it may not be acceptable or sensible to serialise the processing of events by waiting for the system to reach a new stable global state after each event before presenting the next event. However, we work on the basis that the functional behaviour of transactional systems is a separable concern from the timing or performance behaviour. Thus once a model has been prototyped successfully to confirm correct functional behaviour, software with the same functional behaviour and required performance characteristics can be created by combining the behavioural model with standard transaction processing concurrency strategies and load distribution/ balancing techniques. Structure of this PaperThis paper is organised as follows: In Section 2 we provide a summary of the definition of the protocol machine, as described in our earlier paper, Protocol Modelling [Mcn05]. This summary is intended to provide the reader with enough understanding of the underlying theory to follow the rest of the current paper. In Section 3 we describe a concrete syntax for protocol machines using state transition diagrams, and provide a small example. In Section 4, we discuss the reason for modelling different kinds of behaviour, thus motivating our idea of different behavioural types. We go on to show how protocol machines can be given different semantics, and describe a deontic type system that enumerates the different semantics that may be given to a protocol machine. To illustrate the technique, we extend the example introduced in Section 3. Finally, in Section 5 we provide a view of possible tool support, and how the technique and tool can be used in practice. 2 PROTOCOL MODELLINGProtocol MachinesThe basis of the modelling approach is an abstract construct called a protocol machine. Protocol machines have the property that large, complex protocol machines can be assembled from small, simple ones. We use them to build models of systems that comprise objects and, in this use, the smallest protocol machines are more fine-grained than objects, but the largest represent whole systems. A summary of the definition of a protocol machine follows2:
Composition of Protocol MachinesTwo machines can be composed in parallel to yield a new machine, using a parallel composition semantics essentially the same as that introduced by Hoare in his process algebra, Communicating Sequential Processes (CSP) [Hoa85]. If two machines, m1 and m2, are composed the resultant machine, m3, is defined as follows:
Note that if m3 refuses the event, there is no permanent change to the values of the local states of either m1 or m2, even if one of these on its own were capable of accepting the event. Protocol ModelsA protocol model is an object model built from protocol machines. Composition is used in two ways to build a model. Firstly, an object is defined by one or more machines, composed in parallel. Each of the machines that belong to a given object share an object-id that ties it to the object whose partial definition it represents. Secondly, a model is defined as a set of objects, each with its own unique object id, composed in parallel. The effect of this is that where an event instance involves multiple objects, all of the participating objects must accept the event, otherwise it is refused and no change of state in the system takes place. For instance, in a simple Project Administration system, an event that assigns a person to a project (an "Assign" event) might require that the person is in the state "available" and the project is in the state "active". Presentation of an Assign event would be refused by the model if either the Person or the Project specified in the event were not in the right state. The building blocks for creating protocol models are elementary machines, ones that are not defined as the composition of other machines. The next section describes a syntax for defining the behaviour of an elementary machine. 3 A SYNTAX FOR PROTOCOLConcrete SyntaxIn this section, we describe a state/transition syntax for defining the behaviour of an elementary protocol machine. For each event-type in the machine's repertoire3, a definition must be given of:
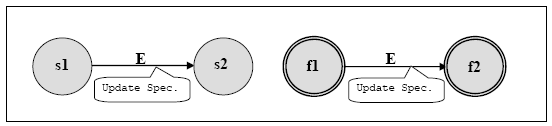
There are two variants of the notation, as shown in Figure 1, each of which is a partial description of a machine.
Figure 1. The Two Notational Variants for Protocol Machines In both variants, the circles represent states of the machine, and the transition represents the effect of an event. In both cases, the diagram represents a successful event acceptance scenario for an event type E in the repertoire of the machine. In the left hand variant, the states "s1" and "s2" are values of a distinguished stored variable (the "state variable") in the local state of the machine. The semantics of this diagram is:
In the right hand variant, the circles (this time with a double outline) represent values that are computed by the machine, using a distinguished function called the machine's "state function". This is a function on the local state and state environment of the machine that returns an enumerated type, of which "f1" and "f2" are two possible values. Again, the diagram represents a successful event acceptance scenario, but with the following semantics:
The full behaviour of a machine is specified by a set of diagrams of the above form. An event presented to the machine is accepted if and only if there is a corresponding success scenario for the event-type. Note the following:
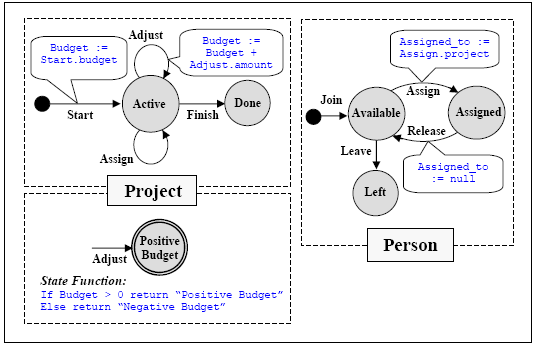
ExampleAs an example, Figure 2 shows possible elementary machine definitions for the simple Project Administration system mentioned earlier.
Figure 2. A basic Protocol Model for a Project Administration System. In this model, two machines are used to define Project and one to define Person. Note the following: • Updates to the local state of the machine take the form x := y. Here x refers to a variable, or slot, of the local state of the machine, and y is an expression computed from the state accessible to the machine and the values of the event attributes. The latter are shown in the form event_name.attribute_name. For simplicity, not all updates are shown. • The fact that the Assign event appears in both Project and Person means that this event cannot take place unless the Project involved is in the state Active and the Person involved is in the state Available. • The second (lower) machine for Project specifies that when an adjustment, which can be positive or negative, is made to the budget of the project, the result of the adjustment must be that the budget exceeds zero, as a zero or negative budget is meaningless. This machine uses the right hand variant from Figure 1 but, as we are not interested in the state before the Adjust, no starting state is needed. 4 DEONTIC BEHAVIOUR TYPESIndicative and Optative DescriptionsWhen modelling, it is possible to distinguish between two types of description: those that refer to the application domain independently of the existence of the system, and those that pertain to the role of the system in its interaction with the domain. The motivation for this distinction has been made, for instance by Jackson and Zave [Jac95] and Parnas [Par95]. Jackson uses the word indicative to refer to descriptions of the domain, and optative to refer to descriptions pertaining to the role of the system. In general, both kinds of description are necessary when developing a system. The reason for making indicative descriptions is that a system tracks the states of an external reality4, in the sense that a project administration system tracks projects and people, a stock control system tracks stock levels, and an air traffic control system tracks aircraft. The system is then able to provide its users with information about the reality:
When designing a system it is necessary to understand what states are possible in the domain because the system, in order to track the reality, must be able to mirror these states. Indicative models describe these states. But a system will also enforce, or help to enforce, user defined rules or policies:
These reflect requirements of the system, as they describe what we want to be true when the domain and the system interact, and are the subject matter of optative descriptions. Violation of the rules and policies contained in optative descriptions is both meaningful and possible, the degree of actual compliance depending on the nature of the interaction between the system and the domain. Where a system is embedded and controlling a mechanical domain, such as a computer based electro-mechanical speed limiter connected to the engine of a bus, there is reasonable guarantee that the speed will remain within the desired limit. Where humans are involved, for instance if the computer simply displays a warning to the driver if the bus is going too fast, there is no such guarantee. In particular, when designing business systems that are to be embedded in human organisations, it is not appropriate to make any assumptions about the likelihood or extent of compliance. We explore the consequences of this in the following section. Optative MachinesProtocol machines can be used to make both indicative and optative descriptions concerning relationships between states and events. In the discussion so far, and the example shown in Figure 2, we have been using protocol machines to make indicative behaviour descriptions. In the context of indicative descriptions, refusal of an event by a model denotes that the model is unable to ascribe a meaning to the event and is therefore unable to adopt a new stable state. We now extend the use of protocol machines to optative descriptions. Here the semantics of "acceptance" and "refusal" have to be different, as it both possible and meaningful for events to take place that violate the rules of optative descriptions. Instead of causing the event to be rejected as unprocessable, acceptance or refusal by machines with optative semantics causes feedback to the source of the event (a user, or possibly another system) on the event's appropriateness. The form of such feedback is discussed later, in Section 5. There are two types of optative machine semantics, corresponding to whether feedback is associated with acceptance or refusal, as shown in the table below.
The second column indicates which disposition (accepted or refused) of an event by a machine causes feedback to be returned to the source of the event. The third column maps the two types of machine to natural meanings, which we refer to as deontic semantics as they correspond roughly to the ideas of "obligatory" and "forbidden" (or "encouraged" and "discouraged") in deontic logic systems5. Together with machines that describe indicative behaviour (which we refer to as Type E6) we now have a vocabulary of three deontic types of machine (E, D, and A) for describing object behaviour. It is to be emphasized that refusal of an event by a Type D or Type A machine does not prevent the event being processed by the model – only machines with deontic type E can do this. Form and Syntax for Optative MachinesOur general goal is to use the same syntax, as described in Figure 1, for machines of all deontic types, as this facilitates changing the type of a machine in the context of developing behaviour models. However the different nature of optative machines (Types D and A) means that they are subject to special rules of form and syntax, which we now describe. Suppose that an object o is described by a heterogeneous set of machines of all three deontic types. Without loss of generality, we can take it that o is described by exactly three machines (mE, mD and mA), one of each type. This is because:
The two rules that must be observed if the model of o is to be well formed are: The first of these rules states that the repertoire of the optative machines is a subset of the repertoire of the indicative machine. In other words, the optative machines m D and m A do not introduce any new repertoire (event-types) for the object o, but only qualify the event behaviour already defined in m E through the feedback they provide. The second rule says that the optative machines have no local state. This is because optative machines are purely advisory and it is not appropriate for the permanent state of the model to reflect whether the advice was taken or not8. This rule has two consequences for the syntax used to describe optative machines:
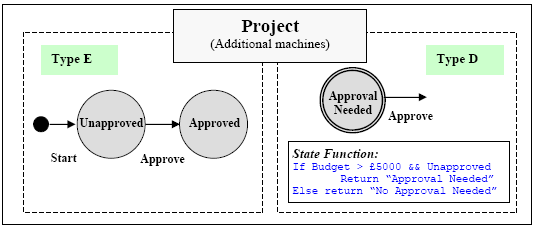
Example (Continued)As an example, Figure 3 shows two further machines for the Project Administration system described in Section 3 (Figure 2).
Figure 3. Additional Machines (Type E and Type D) for Project. Both these machines belong to the Project object, which already had 2 machines in Figure 2 (both Type E) and now has 4 machines (three Type E and one Type D). The two new machines in Figure 3 model project approval, whereby a project that has a budget over £5000 has to be approved by senior management. The left hand machine is Type E, and specifies that the Approve event is only meaningful for a Project that is unapproved. Note, however, that it does not say that approval must happen. The right hand machine specifies that approval is desired if the Project is currently unapproved and the budget exceeds £5000. Note that the state of the left hand machine is part of the state environment of the right hand machine, allowing the latter to access the former in its state function. Now we suppose that the Project object has a method self.estimated_cost() that calculates the estimated cost of the project based on its duration and the people assigned to work on it. This requires that the model has some extra attributes (e.g., duration for Project and daily rate for Person) which we have not shown. Figure 4 shows a further machine for Project, determining when it is allowed to add resources to a Project.
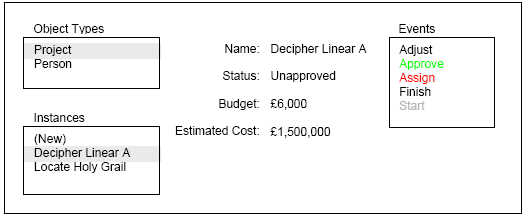
Figure 4. Additional Machine (Type A) for Project. The rule described by this machine is that assignment of a Person to a Project is not allowed unless the estimated cost of the project both before and after the assignment is less than the budget. This machine has deontic type A so will not prevent assignment, but will provide feedback if the rule is broken. The definition of the Project object now comprises 5 machines, 3 of Type E and one each of Type D and Type A. Part of the motivation of the modelling approach described is that it is possible to explore different behaviours, using a prototype system yielded by direct execution of the model, by changing the deontic types of the machines and hence the "strength" of the rules they represent. For instance, changing the type of the machine in Figure 4 from Type A to Type E (indicative) will cause breaching of the budget by assignment of a Person to a project to become impossible in the system. Whether constraints are to be treated as indicative or optative can have a significant effect on the form and behaviour of a model: for instance, the model of Person in Figure 2 contains the indicative constraint that a Person is only assigned to one Project at one time. Perhaps this is the company policy, but is it really correct to model it as an indicative constraint? 5 TOOL SUPPORTAs mentioned in the introduction, our interest is in using behavioural models to explore requirements early in the systems development process. We do this by using tools that yield executable prototypes from behavioural models of the form described in this paper. A full discussion of tool support is beyond the scope of this paper, but one issue of relevance to deontic semantics is how the information about whether events are possible, allowed and desired is presented to the user. Agility and speed in the requirements modelling process requires that tool support delivers a prototype from a model as easily and quickly as possible. One capability in a tool that contributes significantly to this is the ability to provide a user interface for a prototype automatically, so that no user interface programming is required in order to be able to run a model for demonstration to or evaluation by users. In this section we show how the semantics of the different deontic types can be manifested at the user interface in a standard way that can be derived from the model without further programming. Figure 5 shows the appearance that the user interface might take when running the Project Administration model.
Figure 5. User Interface for the Project Administration model. The boxes on the left hand side allow the user to browse the contents of the model. The user selects an Object Type (Project in this case) whereupon a list of instances is displayed below. A key aim of prototyping is to make the behaviour of the model accessible and understanding to non-technical stakeholders who do not necessarily understand the modelling formalisms used. For this reason, the user interface presents the model in terms of objects and events but hides the internal machine level structure of the objects. On selecting an instance in the list on the lower left side, the attributes of that instance are shown to the right along with a list of the events that are available on that instance. The list of available events is generated from the model and colour coded as follows:
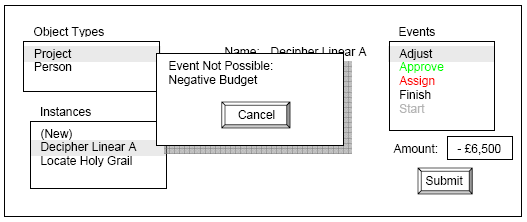
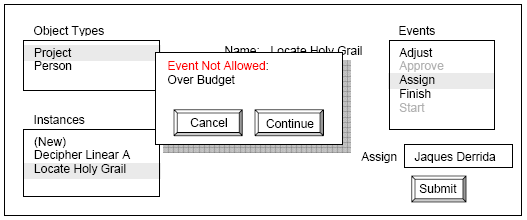
Events in grey are disabled, so selecting one of these has no effect. When an event that is not grey is selected from this list, controls are displayed to allow the attributes of the event to be entered and the event submitted for processing. The colour coding is based on the constraints imposed on the event by the current stable state of the model. A different treatment is needed for constraints imposed by the outcome of an event, as is the case for the lower left hand machine in Figure 2 and the machine in Figure 4. The approach here is to display a model alert after submission of the event to inform the user of violation of the constraint. Figures 6 and 7 show examples.
Figure 6. User Interface after attempt to Adjust the Budget. Figure 6 shows an attempt to reduce the budget of a project below zero, violating the post-constraint specified in the Type E machine in Figure 2. A model alert is displayed informing the user that the event is not possible. The only option presented is Cancel and this causes the event to be abandoned so that the state of the model is unchanged and the budget remains at £6,000.
Figure 7. User Interface after attempt to Assign a new Person to a Project. Figure 7 shows the result of an attempt to assign a new person to a project that breaches the budget. In this case a model alert is generated because the state resulting from the transition is not "Within Budget" as required by the post-constraint in Figure 4. The alert gives the user two options: either to cancel the event, in which case the assignment of Jacques Derrida does not take place, or to continue in which case it does. This is in accordance with the semantics of optative descriptions, namely that violation of the constraint does not prevent processing. The handling of violation of a Type D post-constraint is handled in a similar way. If such a constraint is violated a model alert appears with a green message "Event not Desired" and giving the user the same two options, either to cancel or continue. Together, the capabilities described here provide a default implementation of the different semantics supported by the modelling language, allowing deontic behaviour to be exercised and explored. Because the tool creates a user interface that is entirely model driven, both in its appearance and behaviour, it supports rapid iterative behavioural prototyping. In practical use this helps ensure high quality modelling, both because the realised executable semantics leave little room for ambiguity or diversity of interpretation and because it enables people who are not comfortable with abstract modelling notations to participate in reviewing emerging models. FOOTNOTES1 We will use "event" for event instance throughout this paper. Where we need to refer to an event type, we will use the explicit term. 2 This is a simplification. For a full discussion, see [Mcn05]. 3 The specification of a repertoire entry actually requires more than an event-type. See [Mcn05] for a full discussion. 4 Not all systems do this. This is not true, for instance, of authoring systems such as word processing or CAD. 5 See, for instance, Hilpinin [Hil71]. 6 E stands for Essential, an alternative term meaning the same as Indicative. 7 A machine with an empty repertoire ignores all events presented to it. 8 Except, perhaps, that it should be logged for audit purposes. We assume that such logging is a separate aspect not of concern in the kind of behaviour modelling we describe here. REFERENCES[Coo94] Cook, S., and Daniels, J., Designing Object Systems – Object-Oriented Modelling with Syntropy, Prentice Hall International, 1994. [Hil71] Hilpinen, R., Føllesdal, D., "Deontic Logic: An Introduction" in Deontic Logic: Introductory and Systematic Readings, D. Reidel, Dordrecht 1971, pages 1-35. [Hoa85] Hoare, C., Communicating Sequential Processes, Prentice-Hall International, 1985. [Jac83] Jackson, M., System Development, Prentice Hall 1983. [Jac95] Jackson, M., and Zave, P., "Deriving Specifications from Requirements: An Example" in ICSE17, vol. 1995, pages 15-24. [Mcn05] McNeile, A., and Simons, N., "Protocol Modelling" in The Journal on Software and System Modeling, vol. 5, no. 1, April 2006, pages 91-107. [Mcn03] McNeile, A., and Simons, N., "State Machines as Mixins" in Journal of Object Technology, vol. 2, no. 6, November-December 2003, pages 85-101. http://www.jot.fm/issues/issue_2003_11/article2/ [Met07] Metamaxim website, www.metamaxim.com. [Par95] Parnas, D., and Madey, J., "Functional Documentation for Computer Systems Engineering" in Science of Computer Programming (Elsevier) vol 25, no.1, October 1995, pages 41-61. About the authors
Cite this article as follows: Ashley McNeile, Nicholas Simons: "A Typing Scheme for Behavioural Models", in Journal of Object Technology, vol. 6, no. 10, November-December 2007, pp. 81-94 http://www.jot.fm/issues/issue 2007_11/article2/ |
||||||||||||||||||||||