|
Inheriting from a Common Abstract Ancestor in Timor J. Leslie Keedy, Gisela Menger and Christian Heinlein |
REFEREED ARTICLE PDF Version |
Abstract
A particular case of multiple inheritance, involving a family of related types with a common abstract ancestor, is examined, and a substantial example, involving five abstract and nine concrete collection types, is presented. The separation of types and implementations, together with the separation of subtyping and code re-use, results in a clearly structured and easily intelligible type library which allows extensive polymorphic use of collections at the type level. A full implementation of only one of these types, together with a few additional trivial code units, can be re-used to implement all nine concrete types. The paper concludes by describing how the binary methods and constructors can also be easily and efficiently designed and implemented.
1 INTRODUCTION
Multiple inheritance provides a number of challenges for the design of object oriented programming languages which affect both subtyping and subclassing. This paper discusses how the programming language Timor1, which is currently under development at the University of Ulm in Germany, supports two related aspects of multiple inheritance. The first concerns the progressive design, using multiple inheritance, of families of related types which have a common abstract ancestor. The second is the implementation of such designs in a way which can maximise the re-use of code.
Timor has been designed specifically with the idea of designing and implementing software components for object oriented systems. By components we, like McIlroy [13], mean general purpose software units which can be designed and implemented by a software components vendor for use in many different application systems. For this reason Timor rigorously separates type definitions, known as type interfaces or simply types, from their implementations. This separation allows a component developer to define a type and then produce different implementations thereof for sale to (possibly different) customers. In this context a distinction between types and their implementations is useful even if in individual application systems a single implementation of any particular type is always used. Consequently in this paper we do not fully address issues raised by the contemporaneous use of different implementations of a single type in a single application or system, although Timor also allows this possibility. Similarly we do not consider how client users select a particular implementation for a type.
The distinction between types and implementations (which, unlike Java classes, are not themselves types) facilitates a similar separation of subtyping from subclassing, thereby allowing issues related to these themes to be handled orthogonally. Timor allows programmers to define derived types which can extend supertypes in a behaviourally conform manner [12] and/or can include base types without implying behavioural conformity. Only variables of supertypes defined by extension can be the object of assignments of their extended subtypes in the traditional sense of inclusion polymorphism [3]. But a type derived by inclusion is not a supertype in this sense.
These features of Timor are described more fully in [10], but only in terms of single inheritance. In the present paper we show how a particular case of multiple inheritance is supported in Timor both at the type and implementation levels.
The standard OO class construct does not distinguish between types and their implementations, with the consequence that multiple inheritance is usually viewed as a code re-use problem. By introducing the idea of interfaces, Java was able to separate issues of multiple type inheritance from multiple code re-use; the former is supported in Java, the latter is not [1]. The fundamental distinction which is made in Timor between types and implementations allows the two issues not only to be clearly separated, but also simplifies support for multiple code re-use.
Section 2 distinguishes four kinds of multiple type inheritance, three of which can, at least partially, be modelled using aggregation rather than inheritance, and explains why only the first case is discussed in this paper. Section 3 discusses the kinds of method collisions which can occur in the first case. In section 4 an extended example from the Timor Collection Library is described, which is used throughout the paper. This leads to the formulation of two type inheritance rules for Timor in section 5. Sections 6 and 7 then show how constructors and binary methods are supported in Timor, while section 8 describes how these can include abstract algorithms.
From section 9, which introduces the concept of multiple implementations in Timor, the focus moves to implementation techniques. Section 10 shows how in some cases any of the implementations of a type can be re-used in the implementation of some other (possibly unrelated) type, while section 11 discusses how individual implementations can be used, a technique which can, but need not, be used to emulate conventional subclassing. Section 12 shows how a few further trivial code units can be defined, which can be re-used to implement the duplication properties of different collection types. Section 13 summarises the code re-use rules. Techniques for implementing binary methods and constructors are then introduced in sections 14 and 15. Section 16 concludes the paper.
2 MULTIPLE TYPE INHERITANCE
Multiple inheritance at the type level can be regarded primarily as a modelling tool. It can be used to model at least four kinds of situations:
- An abstraction (e.g. Collection) can be specialised in different ways (e.g. as an OrderedCollection, a DuplicateFreeCollection). Such specialisation can involve orthogonal properties (here ordering and duplication properties) which can appear in various combinations in actual objects (e.g. Set, List), resulting in diamond inheritance.
- A concrete object type (e.g. Person) can also be specialised in different ways (e.g. as a Student, an Employee). Such specialisation can also involve orthogonal properties which can appear in various combinations in actual objects, also resulting in diamond inheritance (e.g. a StudentEmployee).
- Two or more different object types (e.g. Radio, CassettePlayer) can be combined to form a single new (compound) object type (e.g. RadioCassettePlayer).
- Two or more objects of the same type can be combined to form a single new (compound) object type (e.g. DoubleCassettePlayer). The effect is repeated inheritance.
The basic problem which all of these create is that collisions can occur among the members inherited from two or more parent types. However, each case seems to require a separate approach.
In case a) it usually seems more appropriate to merge colliding members (e.g. a method insert) to form a single member in the new type, because it is the different definitions of methods which express the differences in the types.
Case b) differs from case a) in that the methods inherited at the bottom of the diamond rarely need to be redefined in intermediate types, because they refer to the same concrete object type.
In case c) collisions are more likely to be accidental, so that merging into a single method may not be the ideal answer.
In case d) the use of a single type name is insufficient to disambiguate the names of members.
Case a) differs from cases c) and d) in that the latter can at least partially be modelled without using inheritance at all. Instead they can be defined by aggregation, i.e. the object types to be inherited in the new type can instead be regarded as named component variables of the new type. Thus for example a RadioDoubleCassettePlayer object can in principle be modelled either as inheriting a radio and two cassette player objects or as having such components declared as variables. The aggregation approach solves the naming problem but requires the programmer to forgo some advantages of inheritance. We refer to examples falling into the categories (c) and (d) as multiple component inheritance.
Case b) can also be partly modelled using aggregation, although this is probably unusual in current OO practice. For example separate types Studying and Employed can be defined which do not inherit from Person, but with all the new members appropriate to a student or an employee. These types can then be included in new types Student, Employee and/or StudentEmployee by aggregation. Hence case b) is borderline, and can be treated either as multiple component inheritance or abstraction inheritance (i.e. as an example of case a)).
To find a mechanism for realising the advantages both of multiple component inheritance and of aggregation involves quite separate techniques from the issue of unifying members which have been inherited from a common ancestor via different paths. Both have interesting facets and both find innovative support in Timor. In the present paper we address the issue of multiple inheritance from a common ancestor. Timor's approach for handling multiple component inheritance is based on aggregation, enhanced by some new techniques which will be described in a future paper.
3 HANDLING COLLISIONS IN TIMOR
In Timor all the members of a type definition are formally considered to be methods 2. Consequently the discussion of collisions can be confined in the present context to method collisions.
Following the Java approach [1] to method collisions, Timor distinguishes between collisions merely in the names of methods and collisions of method signatures. Collisions of complete method signatures are treated as cases of redefinition, while collisions merely in the names of methods (i.e. where the signatures otherwise differ) are treated as overloading. When overloading occurs, each inherited method is considered to be a separate method. Thus discussions of collisions in the sequel refer to cases where the method signatures are indistinguishable.
4 AN EXAMPLE: THE TIMOR COLLECTION LIBRARY
As a realistic example of multiple inheritance from a common abstract ancestor we use that part of the Timor Collection Library (TCL) which, following the concept developed for Collja [6, 7, 14], defines the organisation of general collections according to the following orthogonal properties of their elements:
- duplication of elements in three forms:
- duplicates are allowed,
- duplicates are ignored,
- duplicates are signalled as exceptions.
- ordering of elements in three forms:
- unordered,
- user-ordered,
- sorted by user-defined criteria.
The TCL thus has nine concrete collection types, reflecting all the combinations of these properties. These are as follows:
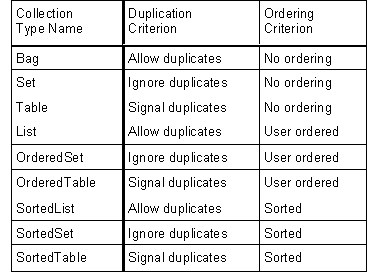
To facilitate their polymorphic use with a high degree of flexibility there are also five abstract nodes:
- the root type Collection (which serves as a polymorphic supertype for all collections);
- the type DuplFree (derived from Collection, a polymorphic supertype for all collections which may not contain duplicate elements),
- the type Ordered (derived from Collection, a polymorphic supertype for all ordered collections),
- the type UserOrdered (derived from Ordered, a polymorphic supertype for all user ordered collections) and
- the type Sorted (derived from Ordered, a polymorphic supertype for all sorted collections).
The complete structure is illustrated in Figure 1.
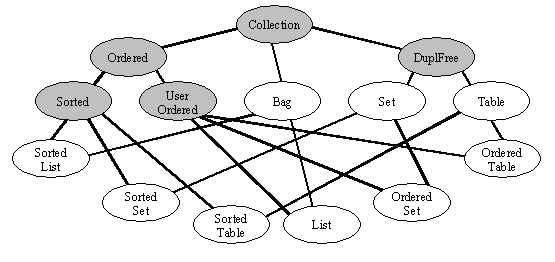
Figure 1: Structure of the Timor Collection
In order to guarantee behavioural conformity all the common methods of all collection types are initially defined in Collection with a maximum of behavioural flexibility. Thus its (abstract) method insert, for example, does not define
- how an insertion affects the ordering of the collection,
- whether the insertion will be successful if it involves inserting a duplicate,
- whether an exception will be thrown to indicate a duplicate (but it defines an exception DuplEx which might be thrown).
An abstract type with such non-deterministic methods is designed to allow a maximum of polymorphism. In derived types the actions of the insert method are specified more precisely, depending on the node in question. Thus the insert method of the abstract type UserOrdered defines that insert appends the element at the end of the collection (and adds new methods for inserting at other positions) but without defining its duplication properties further. On the other hand the insert method of the concrete type Bag is defined without specifying ordering, but indicating that duplicates are accepted (with the effect that the exception DuplEx can be removed from Bag's insert method).
Such redefinitions of methods must be reflected by listing them in a redefines clause of a derived type. As the first version of Timor does not support a formal specification technique, only the headers of such methods are listed, but we intend that a later version will also allow the changes (and of course the original methods) to be more formally specified. Sometimes a redefinition can lead to a change in the method header (e.g. where an exception defined in a parent type may not be thrown in a derived type, cf. Collection with Bag), but in many cases the method header remains the same (though hopefully programmers will be encouraged to document the redefined behaviour in comments).
The redefinitions described above are illustrated in the following simplified example3:
|
abstract type Collection { |
|
|
op void insert(ELEMENT e) throws DuplEx; |
|
|
} |
|
|
abstract type UserOrdered extends Collection |
|
|
redefines { |
|
|
op void insert(ELEMENT e) throws DuplEx; |
|
|
} |
|
|
{ /* new methods for inserting/removing |
|
|
elements at different positions */ |
|
|
} |
|
|
type Bag extends Collection |
|
|
redefines { |
|
|
op void insert(ELEMENT e); |
|
|
} |
|
|
{ /* new method headers */ |
|
|
} |
|
|
type List extends Bag, UserOrdered |
|
|
redefines { |
|
|
op void insert(ELEMENT e); |
|
|
} |
|
|
{ /* new method headers */ } |
|
An important advantage of redefines clauses in Timor types is that they indicate (independently of an implementation) whether and where methods of a common ancestor have been redefined in intermediate nodes in the type hierarchy.
5 TYPE INHERITANCE RULES
We are now in a position to formulate the following type inheritance rules:
redefines {
Type Inheritance Rule 1: If in a derived type multiple methods with the same signature4 are derived from a common ancestor, they are treated as a single method (unless they have different return types, in which case a compile time error arises).
Type Inheritance Rule 2: If the definitions of such methods differ (i.e. if one or more of them has been redefined differently from the definition in their closest common ancestor), they must also be listed in a redefines clause in the type being defined.
Rule 1 is defined in terms of a common ancestor in order to clarify that it does not apply to all cases where methods have the same signature, thus leaving scope for a different definition which might suit multiple object and repeated inheritance.
Rule 2 in effect requires that conflicting definitions are clarified. Where a definition in one of the ancestors can be used in the new type this can be signalled by the use of the keyword from followed by the name of a type, e.g.
|
redefines { |
|
|
op void insert(ELEMENT e) from UserOrdered; |
|
|
} |
|
6 CONSTRUCTORS
Constructors can be declared in Timor types. They deviate from the Java style in order to allow flexibility in their names and in their parameters. The keyword maker introduces each constructor, e.g.
maker Bag init();
// makes a new Bag object
maker Bag intersect(Bag b1, b2);
// returns intersection of b1 and b2
We refer to constructors such as intersect, which have parameters of their own type, or of a supertype, as binary makers. If a concrete type does not have an explicitly defined constructor, the compiler supplies a parameterless constructor with the name init.
An interesting example of a binary maker is introduced in the type List.
maker List reverse(Ordered c);
This can accept any ordered collection (i.e. both user-ordered and automatically sorted collections) and create a List instance containing its elements in reverse order.
Constructors are needed only in concrete types, since their purpose is to construct actual instances of types, and in OO languages they are normally not inherited. However Timor provides a mechanism for predefining constructors in abstract and concrete types. Such predefined constructors are then "inherited" in derived types.
A predefined constructor can be recognised by the use of the keyword ThisType as the type name for the return type of a constructor. The TCL has two such constructors, declared in the abstract type Collection, i.e.
|
abstract type Collection { |
|
|
maker ThisType init(); |
|
|
} |
|
The first of these is a normal parameterless constructor. Although declared in Collection it cannot be invoked to produce a Collection instance, because abstract types cannot be instantiated. But it predefines that any concrete type derived directly or indirectly from Collection has such a constructor, called init. Thus the TCL type Bag automatically has a constructor:
maker Bag init();
Similarly each of the concrete types derived from Collection has a constructor convert with a parameter of type Collection, e.g.
maker Set convert(Collection c);
The parameter is of course polymorphic, allowing any kind of collection instance in the type hierarchy to be passed to the constructor as a parameter. Thus the code sequence
Bag b = new Bag.init();
...
Set s = new Set.convert(b);
produces a new Set instance containing the same members as appear in the Bag b (but with duplicates removed).
In the type Collection several other binary makers are predefined, e.g.
maker ThisType merge(Collection c1, c2);
// returns merge of c1 and c2 as
// a collection of the current type
maker ThisType intersect(Collection c1, c2);
// returns intersection of c1 and c2 as
// a collection of the current type
maker ThisType difference(Collection c1, c2);
// returns difference of c1 and c2 as
// a collection of the current type
The maker merge serves as a union operation for sets, a concatenation operation for lists, etc.
If a predefined maker is derived from more than one base type leading to a collision of the signatures, the two definitions are merged into a single predefined maker. Where the signatures differ the Java rules for overloading apply.
7 BINARY METHODS
Timor types do not support the concept of static methods or fields. The effects of Java static declarations are achieved in other ways5. One such possibility is relevant to this paper, namely the introduction of binary methods in Timor types. A binary method carries out operations on multiple existing instances of a type. They are typically used to compare instances, e.g.
binary boolean equal(Set s1, s2);
binary boolean includes(Set s1, s2);
An important advantage of Timor's binary methods is that they provide a vehicle for implementing binary operations, in the sense described in [2], without creating the problems associated with binary instance methods.
Like makers, binary methods can be predefined for derived types. In this case the keyword ThisType is used to define parameters which are covariantly adapted to the current type.
In this respect they are similar to predefined makers, but with one significant difference. Whereas a predefined maker only exists as a real constructor in concrete derived types, binary methods not only covariantly predefine methods for concrete types; they also exist as real methods in the abstract types in which they are defined or derived. This is one of several reasons for distinguishing the two constructs.
In the TCL several binary methods are defined in the type Collection, e.g.
binary boolean equal(ThisType c1, c2);
binary boolean includes(ThisType c1, c2);
What this means is that each abstract and each concrete type derived from Collection has these methods, e.g. List has methods
binary boolean equal(List c1, c2);
binary boolean includes(List c1, c2);
and Bag has methods
binary boolean equal(Bag c1, c2);
binary boolean includes(Bag c1, c2);
In this case the parameters are not instances of Collection which are intended to be used polymorphically, although derived types of the actual parameter types can of course be passed to the actual methods in accordance with the normal polymorphism. For example because List is a derived type of Bag, a List instance can be passed to the Bag.equal method, but a Bag instance cannot be passed to List.equal.
8 ABSTRACT ALGORITHMS
It is not always obvious, in examples such as the TCL, how binary methods and makers are intended to function. For example how does the predefined maker which appears in every collection type convert from all other collection types to its own particular type? What does a comparison for equality mean?
To help clarify such questions Timor allows types to include abstract algorithms in the definitions of makers and binary methods. An abstract algorithm can use the methods of its type, but recourse to actual implementations of the type is not allowed.
One way of looking at an abstract algorithm is as a specification of a maker or a binary method, expressed in terms of the basic operations on a type. Alternatively it can be viewed as an algorithm which a client could write himself by using the methods of the type. A further useful viewpoint will become evident in sections 14 and 15.
The following is a slightly simplified example of an abstract algorithm, which defines a general algorithm for the "conversion" maker in the type Collection:
|
maker ThisType convert(Collection c) { |
|
|
Enumeration enum = c.elements(); |
|
|
|
|
} |
|
|
} |
|
We see that it is defined to iterate over all elements of its parameter, using its own insert method in an attempt to insert it into the new collection.
Because Collection is abstract this maker does not really exist, it merely predefines an algorithm for its derived types. Thus the effect of the insert method invocation depends on the type for which the maker is actually invoked. In Table, OrderedTable and SortedTable invoking the insert method can result in a duplicate exception being thrown. The algorithm shows that this is ignored, allowing conversion of instances of these types to occur without an exception being thrown. If on the other hand the type in question is an ordered type the actual insert method of the type will cause the element to be placed in its appropriate place (either automatically sorted or appended).
Abstract algorithms for binary methods are similar. In this case they invoke the methods of their parameters, as the following example shows:
|
binary boolean equal(ThisType c1, c2) { |
|
|
if (c1.size() != c2.size()) return false; |
|
|
elem = enum.nextElement(); |
|||
|
|
|||
|
} |
|||
|
} |
|||
The algorithm first checks that the two collections have the same number of elements then that there are the same number of occurrences of each element in both.
Like the algorithm in the maker convert this algorithm is predefined for derived types, but unlike the former it is a "real" algorithm, in the sense that binary methods, unlike makers, also exist for abstract types. In other words there is a real binary method:
binary boolean equal(Collection c1, c2);
defined in the abstract type Collection. Using this algorithm any two instances of (concrete) collection types can be compared for equality.
Derived types always inherit predefined makers and binary methods defined in their supertypes, but they can redefine the algorithms. For example in Bag and Set (neither of which throw duplicate exceptions) the maker convert can be simplified (in a redefines clause) to:
|
maker ThisType convert(Collection c) { |
|
|
Enumeration enum = c.elements(); |
|
|
} |
|
The possibility of redefining abstract algorithms in derived types raises the question: Which algorithm is valid when different versions exist in predefined methods which are all inherited in a derived type? In this case the definer of the type has the choice of selecting one of the existing algorithms or defining a new algorithm. Thus in List, which is derived from Ordered and from Bag, the algorithm can be selected as follows:
|
type List extends Bag, UserOrdered |
|
|
binary boolean equal(ThisType c1,c2) from UserOrdered; |
|
|
} |
|
|
{ /* new method headers */ |
|
|
} |
|
9 IMPLEMENTATION TECHNIQUES
Each abstract type in Timor can have zero or more implementations, each concrete type needs one or more. An implementation can, regardless of any relationship between its own and other types, have one of several forms:
- It can have a completely new implementation. This is well suited to the information hiding principle [15-17]. The new implementation of the methods of supertypes must conform with the specifications of the supertypes (where relevant as redefined in the derived type). The implementation of new and redefined members must conform with the specification of the derived type.
- An implementation can re-use implementations of other types (indicated by the keyword reuses). In contrast with standard OO practice a subtype relation between the type of the new implementation and those of the re-used implementations need not exist. Thus code re-use can be completely decoupled from subtyping and from the inclusion of interfaces.
- A reuses clause can designate a specific implementation to be re-used. Alternatively, it can designate a type, any of whose implementations can be re-used (at the level of the public members). The first case typically reflects the conventional object oriented style of code inheritance, while the second leads to a quite different style of code re-use.
- An implementation can also re-use typeless implementations, i.e. implementations which are defined independently of a specific type and which cannot themselves be used as types. This case is also indicated by the keyword reuses.
- A type can be mapped to another type, and in this way re-use its implementations, without implying a relationship between the two types. This technique is described in [10] but not discussed further in this paper.
10 RE-USING ANY IMPLEMENTATION OF A TYPE
With the kinds of types under discussion it is often desirable to provide alternative implementations, based for example on an array, on various forms of linked lists, etc. We now describe how Timor allows the re-use of any implementation of a type in implementations of a different type, without implying a subtyping relationship.
We begin with an implementation of the TCL type List as if it were a completely independent type (cf. section 9 a.):
|
impl ArrayList of List { |
||
|
impl ArrayList of List { |
||
|
return currentSize; |
||
|
} |
||
|
op void clear() { |
||
|
currentSize = 0; |
||
|
} |
||
|
op void insert(ELEMENT e) { |
||
|
// defined to append e |
||
|
} |
||
|
op void insertAtPos(ELEMENT e, int pos) |
||
|
throws OutOfBoundsEx { |
||
|
|
||
|
setInArray(e, pos); |
||
|
} |
||
|
op void setInArray (ELEMENT e, int pos) { |
||
|
// an internal method to insert e |
||
|
} |
||
|
... |
||
|
} |
||
The OutOfBoundsEx exception is a checked exception which appears in the type definition for insertAtPos, a method first introduced in the abstract node UserOrdered.
Because a simple array implementation is used, the possibility arises that it can become full. Hence in both insert and insertAtPos an exception (FullEx) is thrown, which does not appear in the type definition. This is an unchecked exception. The issue of restrictions which can appear in individual implementations of a type is taken up in section 14, where it is shown how the value of maxSize can be passed as an implementation parameter without affecting the type definition.
As no reuses clause appears, and as List is a concrete type, the implementation must be complete. By definition it conforms with the information hiding principle. Many equivalent implementations of List, e.g. SingleLinkList and DoubleLinkList, can be programmed.
Leaving aside until later the question of makers and binary methods, it is evident that all such implementations of the instance methods of List can be re-used as implementations of Bag. The insert method in List is specified to append elements and to accept duplicates. That of Bag inserts elements without defining a position and it also accepts duplicates. Hence any implementation of List fulfils the specification of Bag. So implementing Bag costs virtually nothing:
impl NewBag1 of Bag reuses List {
}
The reuses clause can name one or more types, indicating in this example that any implementation of List can be re-used as an implementation of Bag 6.
What the reuses clause actually means is described in section 13. Its application here is that all matching methods of Bag use the implementation in the specified "implementation" type (here List). A match is defined as a method in the re-used unit with the same signature and return type, and with either the same exceptions or a subset thereof.
Any additional public methods which the latter implements, but which are not needed, cannot be invoked by clients. Any members not needed by the implementation can be removed. In this example methods such as insertAtPos are redundant in implementations of Bag.
This example shows how a subtyping relationship and a subclassing relationship are often the reverse of each other. By separating these issues Timor can easily cope with the two.
11 RE-USING INDIVIDUAL IMPLEMENTATIONS
A reuses clause can optionally nominate individual implementations. This technique can (but need not) be used to mimic conventional incremental OO subclassing. One could begin by implementing the abstract type Collection, for example by defining data structures and programming those methods which are valid for implementations of all the subtypes (e.g. size, clear). But the definition of methods such as insert, which are non-deterministically specified in Collection and require different implementations in different derived types, will be incrementally coded in an implementation of the corresponding type.
The same technique can be used where a subtyping relationship does not exist. We now show how it is used in the TCL to implement SortedList. The latter differs from List primarily in that its insert method uses some criteria7 for automatically sorting elements in the list. For any particular implementation most of the required code will be identical to that for List. This is clearly another case for code re-use. Here is how it can be defined for an array implementation:
|
impl ArraySorted of SortedList reuses ArrayList |
||
|
op void insert(ELEMENT e) { |
||
|
// defined to sort e |
||
|
} |
||
|
... |
||
|
} // end of redefined methods |
||
|
op void sortIntoArray(ELEMENT e) { |
||
|
.../* more new methods */ |
||
This implementation "borrows" all the data structures and methods which it needs from the List implementation ArrayList (see section 10). The overrides clause indicates which methods are overridden in a re-used implementation, and provides a new implementation for them. (It could use a "super" mechanism to invoke the original methods, though that is not appropriate here.) Again redundant methods (e.g. insertAtPos) can be pruned where appropriate.
In this example we see how two subtypes of the same behavioural supertype (Ordered) can be implemented by one re-using the code of another8. Further implementations of SortedList could be produced in the same way, by re-using SingleLinkList, DoubleLinkList, etc.
We have now potentially produced a number of implementations of each of the concrete types List, Bag and SortedList, the three types which accept duplicates. Next we consider how implementations of the six DuplFree types can be produced.
12 IMPLEMENTING THE DUPLICATION PROPERTIES
The duplication properties of the collection types are orthogonal to their other properties. Providing new code for each implementation on an individual type basis (e.g. corresponding to the incremental subclassing style) is therefore a combinatorial problem. A better approach is to provide a separate algorithm for each case, which can be re-used in combination with implementations for SortedList and List to implement the remaining concrete types. This aim can best be achieved by providing appropriate mechanisms for checking whether an attempt is being made to insert a duplicate into a collection and if so take the appropriate action.
With this aim in mind we begin with a view interface9 which provides the minimal interface needed for checking for duplicates, and then ignoring these when the insert method is invoked (i.e. relevant for implementing Set, OrderedSet and SortedSet):
|
view Insert { |
||
|
op void insert(ELEMENT e); |
||
| } |
||
Based on this view a typeless implementation can be coded with a method which handles duplicates by overriding the insert method, as follows:
|
impl DuplIgnore requires Insert |
||
|
op void insert(ELEMENT e) { |
||
|
if (!^Insert.contains(e)) ^Insert.insert(e); |
||
|
} |
||
|
} |
||
The requires clause indicates that this implementation is intended for use in an implementation of a type which also implements Insert. Invocations of the methods of Insert are indicated, as when an implementation invokes methods of a reused implementation, with the hat (^) symbol. In this particular example the typeless implementation not only assumes the availability of an implementation of Insert but it also overrides the method insert.
This implementation can now be re-used, together with any implementations of List or SortedList, to implement Set and SortedSet, as follows:
impl Set1 of Set reuses List, DuplIgnore
{/* no new method implementations*/
}
impl SortedSet1 of SortedSet reuses SortedList, DuplIgnore {
}
As described in section 10, the methods of the type to be implemented are matched with those of the re-used implementations. In this example all are satisfied from the first listed "implementation type".
Reused implementations are also examined for overriding methods which match methods of the type. In this case the overriding method insert in DuplIgnore is matched for both types. However, the requires clause must also be checked, to ensure that all the requirements specified via Insert are met. These requirements must be met by matching the definition with that of the type currently being implemented, not with a particular re-used implementation. As the view Insert was especially designed for this purpose, there is no problem.
Implementing OrderedSet also involves ignoring attempts to insert duplicates via the insertAtPos method. For this purpose we can extend the view Insert, as follows:
|
view InsertPos extends Insert { |
||
|
op void insertAtPos(ELEMENT e, int pos); |
||
|
} |
||
and provide a further typeless implementation:
|
impl DuplIgnorePos requires InsertPos |
||
|
op void insertAtPos(ELEMENT e, int pos) { |
||
|
if (!^InsertPos.contains(e)) |
||
|
|
||
|
} |
||
|
} |
||
which can be used to implement OrderedSet as follows:
impl OrderedSet1 of OrderedSet
reuses List, DuplIgnore, DuplIgnorePos { }
Implementations of Table, OrderedTable and SortedTable follow a similar pattern, differing only in the fact that the detection of an attempt to insert a duplicate results in the exception DuplEx being thrown. Here are the relevant units:
|
view SignalInsert { |
||
|
op void insert(ELEMENT e) throws DuplEx; |
||
| } | ||
|
impl DuplSignal requires SignalInsert |
||
|
op void insert(ELEMENT e) throws DuplEx { |
||
|
if (!^SignalInsert.contains(e)) |
||
|
|
||
|
else throw new DuplEx.init(); |
||
|
} |
||
|
} |
||
This opens the way for the following implementations of the remaining collection types
impl Table1 of Table reuses List, DuplSignal {
}
|
impl SortedTable1 of SortedTable |
|
|
reuses SortedList, DuplSignal { |
|
|
} |
|
|
impl OrderedTable1 of OrderedTable |
|
|
reuses List, DuplSignal, DuplSignalPos { |
|
|
} |
|
13 CODE RE-USE RULES
The rules for code re-use for instance methods can be summarised as:
Type Re-use Rule: If a type is nominated in a reuses clause, any of the implementations of that type can be interchangeably re-used. Explicitly coded methods of the new implementation have no access to the private methods or data structures of the re-used "type implementation".
Implementation Re-use Rule: If an individual implementation is nominated in a reuses clause, explicitly coded methods of the new implementation can access the internal methods and/or data structures of the re-used implementation.
Method Matching Rule: A method match occurs when the signature and the result type in a unit nominated in a reuses clause matches that of the type being implemented and the exceptions in the nominated unit are either the same as, or a subset of, those in the type being implemented.
Method Selection Rule: Methods are selected from the first nominated unit in which a match occurs. (Any unmatched methods must be explicitly coded in the implementation.)
Overriding Rule: Overriding methods which appear in re-used implementations are also matched (according to the Method Matching and Selection rules) and in the new implementation they override the corresponding method selected.
Multiple Overriding Rule: If more than one matching overriding method is found, the overriding takes place in the order right to left. This means that if for the clause reuses A, B, C there is a matching method in A which is overridden in both B and C, at run-time the overriding method in C is invoked and if this invokes its "super" the overriding method in B is invoked, which can in turn invoke the original method in A.
Requires Rule: If a re-used implementation has a requires clause, this must be satisfied by the definition of the type being implemented. This means that for each method of the view there must be a matching method (as defined in the Matching Method Rule) in the type being implemented. (The requires rule has no effect on the multiple overriding rule.)
With respect to the collection hierarchy example, these rules together enable all the instance methods of all the concrete types to be implemented, without any algorithm having been repeated for the entire hierarchy. Next we consider the binary methods and constructors.
14 IMPLEMENTING BINARY METHODS
The implementation of binary methods requires special attention for three reasons. First, these require an implementation in abstract types, such as Collection and DuplFree. Second, in a system which contemporaneously supports multiple implementations of a type, it cannot be assumed that when different instances of the same type are compared they will have the same implementation. Third, although an implementation for one type can re-use code of unrelated types, this by no means guarantees that binary method implementations can also be re-used. For example the instance methods of Bag can be implemented by re-using instance methods of List, but a List comparison for equality, which takes into account (and relies on) ordering, cannot be re-used as a Bag equality method (where ordering is not relevant).
In fact all three issues can be resolved by using abstract algorithms (which can appear in type definitions, see section 8) as implementation algorithms. As the abstract algorithms can only be formulated in terms of invocations of public methods (without recourse to particular implementations) such algorithms are implementation independent and can be used even where instances with different implementations are passed as parameters. Furthermore, different abstract algorithms can be provided for different types. Hence the problem would be solved, were it not for the issue of efficiency.
Abstract algorithms always pay the penalty of invoking public methods. This will often not be as efficient as implementations which can directly access implementation data structures and/or internal methods. To overcome this penalty, Timor supports a mechanism [18] which is a variant of the multimethod technique [2]. This allows an implementor to access the implementation details from his own implementation, but (for information hiding reasons and to keep the mechanism relatively simple and clean) not other implementations of the type.
To illustrate the principle, there are four possibilities when two instances are being compared:
- both parameters have the current implementation,
- only the first has the current implementation,
- only the second has the current implementation,
- neither has the current implementation.
In case d) the implementation programmer has no choice: from his viewpoint the abstract algorithm must be used. To handle the other cases he can write (up to) three different versions of a binary method, each taking best advantage of the parameter(s) with the implementation being coded. At run-time the method dispatcher selects a suitable method from the multimethods available from different implementations (or the abstract algorithm). How this works in detail and how the implementor can access an implementation in such a case, will be discussed in a future paper.
15 IMPLEMENTING CONSTRUCTORS
Constructors raise two issues of relevance here. First, a binary maker (which for example merges information from two other instances to create a new instance of a type) has the same problem of multiple implementations just discussed for binary methods. And the solution is the same: an implementor can write such a constructor as a number of multimethods, from which the method dispatcher selects the best at run-time (whereby in this case the "best" is usually also the one which provides the implementation selected for the new instance, if this is known).
The second issue concerns the need for run-time parameters for a particular implementation which are not defined in the constructors for the type. So far we have given the impression that the TCL array implementation uses a preset constant value (maxSize) to determine the size of the array. This is not a practical solution for a collection library intended for wide general purpose use. But a simple fix which allows a parameter to be passed via a constructor is unsatisfactory. The problem is that this would affect the type definition, although each implementation can have different parameter requirements in this respect (e.g. a linked list implementation possibly requires no parameter, a hash table implementation might require a table length, etc.). This kind of consideration led the designers of Theta to separate constructors from type definitions [11]. With the Timor design, which considers operations such as intersect to be binary makers, extra parameters of this kind would be even more obtrusive. Timor therefore takes up an idea first implemented in Tau [18], which allows (potentially different) extra parameters (not visible at the type level) to be defined in different implementations. A default value can be supplied, or there are various ways in which it can be set explicitly (e.g. in pragmas). A full discussion of the technique will appear in a future paper. The important effect is that different implementations can have different parameters which are not reflected in the type definition, allowing the client programmer to ignore them unless he specifically needs to set them.
16 CONCLUSION
Timor rigorously separates a number of structuring concepts which are often treated simply as different aspects of classes and inheritance in some OO programming languages: types are separated from implementations, behavioural subtyping from interface inclusion, subtyping from code re-use (and therefore subclassing). The advantages of separating orthogonal structuring requirements from each other has been illustrated using a substantial example from the TCL.
Fourteen general collection types (five of them abstract) are presented, defining all combinations of two orthogonal properties:
– duplicates are: permitted, ignored, signalled;
– ordering is: unordered, user-ordered, sorted;
in a single behaviourally conform type hierarchy, designed to achieve a maximum of polymorphism.
These are implemented, using code re-use techniques unrelated to normal subclassing, in only six combinable code units, of which only one requires substantial implementation effort. This implements the type List (a user-ordered collection with duplicates, which can also be used to implement unordered collections without violating behavioural conformity). The second re-uses this but implements SortedList (sorted, with duplicates), while the four remaining code units trivially check for duplicates and either ignore them or raise an exception.
To produce different implementations (as arrays, singly or doubly linked lists, etc.) requires recoding only two of these units (List and SortedList), as any implementation of these can be re-used by the remaining four, in all the required combinations because of a strict adherence with the information hiding principle and appropriately defined code re-use rules.
Constructors and binary methods require special treatment. The mechanisms provided in Timor allow these to be predefined (and so standardised) in abstract types. An implementation-independent technique for defining their operation (abstract algorithms) allows implementations of constructors and binary methods to operate independently of particular implementations, while an adaptation of the notion of multimethods can be used to code more efficient versions in particular implementations.
The discussion of multiple type inheritance was deliberately restricted to a particular class of problems. The question arises whether it can be used in other cases. One such case is diamond inheritance arising from a concrete common ancestor (such as Person, inherited by Student and by Employee, coming together in a type StudentEmployee, see case b) in section 2). The techniques presented here can be used for such cases. However, we prefer to see this kind of modelling, along with cases c) and d) as belonging to a different class of multiple inheritance, which we call multiple component inheritance. This raises quite different issues from those discussed here. For such cases Timor approaches aggregation in a novel way and provides a new form of cast statement which leads to the idea of component polymorphism. These ideas form the subjects of a future paper.
ACKNOWLEDGEMENTS
Special thanks are due to Dr. Mark Evered and Dr. Axel Schmolitzky for their invaluable contributions to discussions of Timor and to the ideas which have been taken over from earlier projects. Without their ideas and comments Timor would not have been possible.
Footnotes
1 The design of Timor has been based, wherever appropriate, on the design of Java. Nevertheless, as will be evident in the sequel, it is structurally quite different, even if the syntax is often identical.
2 Abstract fields and abstract references can appear in type definitions. Formally these are regarded as a pair of methods for setting and getting a hidden value.
3 The qualifier op introduces an operation (which can modify the state of an instance of the type), enq introduces an enquiry (which cannot modify the instance's state). This distinction is important for example for defining qualifying types with bracket routines (cf. [8, 9]) but is not significant for the present discussion. The type ELEMENT can be thought of as any relevant type. Timor supports a generic mechanism along the lines described in [4, 5], but again this is not directly relevant to our discussion and is not described here.
4 As in Java, exception declarations are not considered to be part of the signature of a method.
5 A program, for example, is the instantiation of a type by the operating system.
6 Various mechanisms for selecting an actual implementation will be discussed in a future paper.
7 The criteria are defined by clients using the generic technique of Timor, which is not described here (but see [4, 5]).
8 It would equally be possible first to provide an independent implementation of SortedList and then to reuse its code to implement List.
9 View interfaces typically define a standard set of methods which can be used polymorphically in different types. As is useful in this example they can be defined retrospectively, allowing a limited form of structural type matching, which is statically checked when it is needed. A match occurs with the same signature and return type and a subset of the exceptions.
BIBLIOGRAPHY
[1] K. Arnold, J. Gosling, and D. Holmes, The Java Programming Language, Third Edition: Addison-Wesley, 2000.
[2] K. B. Bruce, L. Cardelli, G. Castagna, T. H. O. Group, G. T. Leavens, and B. Pierce, On Binary Methods, Theory and Practice of Object Systems, vol. 1, pp. 221-242, 1995.
[3] L. Cardelli and P. Wegner, On Understanding Types, Data Abstraction and Polymorphism, Computing Surveys, vol. 17, pp. 471-522, 1985.
[4] M. Evered, Unconstraining Genericity, 24th International Conf. on Technology of Object-Oriented Languages and Systems, Beijing, 1997.
[5] M. Evered, J. L. Keedy, G. Menger, and A. Schmolitzky, Genja - A New Proposal for Genericity in Java, 25th International Conf. on Technology of Object-Oriented Languages and Systems, Melbourne, 1997.
[6] M. Evered, G. Menger, J. L. Keedy, and A. Schmolitzky, A Useable Collection Framework for Java, 16th IASTED Intl. Conf. on Applied Informatics, Garmisch-Partenkirchen, 1998.
[7] M. Evered and G. Menger, Very High Level Programming with Collection Components, Conf. on Technology of Object-Oriented Languages and Systems, Nancy, 1999.
[8] J. L. Keedy, M. Evered, A. Schmolitzky, and G. Menger, Attribute Types and Bracket Implementations, 25th International Conference on Technology of Object-Oriented Languages and Systems, Melbourne, 1997.
[9] J. L. Keedy, K. Espenlaub, G. Menger, A. Schmolitzky, and M. Evered, Software Reuse in an Object Oriented Framework: Distinguishing Types from Implementations and Objects from Attributes, 6th International Conference on Software Reuse, Vienna, 2000.
[10] J. L. Keedy, G. Menger, and C. Heinlein, Support for Subtyping and Code Re-use in Timor, 40th International Conference on Technology of Object-Oriented Languages and Systems (TOOLS Pacific 2002), Sydney, February 2002, in Conferences in Research and Practice in Information Technology Series, vol. 10, James Noble & John Potter (eds), Australian Computer Society Inc., pp.35-43.
[11] B. Liskov, D. Curtis, M. Day, S. Ghemawat, R. Gruber, P. Johnson, and A. C. Myers, Theta Reference Manual, MIT Laboratory for Computer Science, Cambridge, MA, Programming Methodology Group Memo 88, February 1994.
[12] B. Liskov and J. M. Wing, A Behavioral Notion of Subtyping, ACM Transactions on Programming Languages and Systems, vol. 16, pp. 1811-1841, 1994.
[13] M. D. McIlroy, Mass Produced Software Components, NATO Conference on Software Engineering, NATO Science Committee, Garmisch, Germany, 1968.
[14] G. Menger, Unterstützung für Objektsammlungen in statisch getypten objektorientierten Programmiersprachen (Support for Object Collections in Statically Typed Object Oriented Languages), Dept. of Computer Structures: University of Ulm, Germany, 2000.
[15] D. L. Parnas, Information Distribution Aspects of Design Methodology, 5th World Computer Congress, IFIP-71, 1971.
[16] D. L. Parnas, On the Criteria To Be Used in Decomposing Systems into Modules, Communications of the ACM, vol. 15, pp. 1053-1058, 1972.
[17] D. L. Parnas, A Technique for Module Specification with Examples, Comm. ACM, pp. 330-336, 1972.
[18] A. Schmolitzky, Ein Modell zur Trennung von Vererbung und Typabstraktion in objektorientierten Sprachen (A Model for Separating Inheritance and Type Abstraction in Object Oriented Languages), Dept. of Computer Structures: University of Ulm, Germany, 1999.
About the authors
 |
J. Leslie Keedy is Professor and Head, Department of Computer Structures, University of Ulm, Germany, where he leads the Timor language design and the Speedos operating design groups. His email address is keedy@informatik.uni-ulm.de. His biography can be visited at http://www.informatik.uni-ulm.de/rs/mitarbeiter/jlk/ |
|
 |
Gisela Menger received a Ph.D. in Computer Science from the University of Ulm in 2000. Currently she works as a scientific assistant in the Department of Computer Structures at the University of Ulm. Her research interests include programming language design and software engineering. Her email address is menger@informatik.uni-ulm.de. |
|
 |
Christian Heinlein received a Ph.D. in Computer Science from the University of Ulm in 2000. Currently, he works as a scientific assistant in the Department of Computer Structures at the University of Ulm. His research interests include programming language design in general, especially genericity, extensibility and non-standard type systems. His email address is heinlein@informatik.uni-ulm.de. |
Cite this article as follows: J. Leslie Keedy, Gisela Menger, Christian Heinlein: "Inheriting from a Common Abstract Ancestor in Timor", in Journal of Object Technology, vol. 1, no. 1, May-June 2002, pp. 81-106, http://www.jot.fm/issues/issue_2002_05/article2