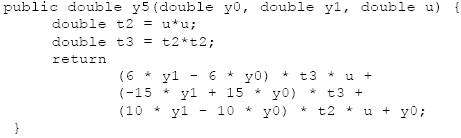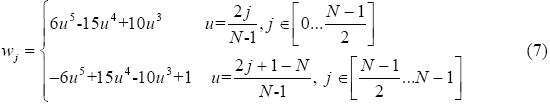AbstractThis paper is part 4 in a series of papers about the Discrete Fourier Transform (DFT) and the Inverse Discrete Fourier Transform (IDFT). The focus of this paper is on spectral leakage. Spectral leakage applies to all forms of DFT, including the FFT (Fast Fourier Transform) and the IFFT (Inverse Fast Fourier Transform). We demonstrate an approach to mitigating spectral leakage based on windowing. Windowing temporally isolates the Short-Time Fourier Transform (STFT) in order to amplitude modulate the input signal. This requires that we know the extent, of the event in the input signal and that we have enough samples to yield a sufficient spectral resolution for our application. This report is a part of project Fenestratus, from the skunk-works of DocJava, Inc. Fenestratus comes from the Latin and means "to furnish with windows".1 INTRODUCTION TO FREQUENCY QUANTIZATION AND LEAKAGEThe DFT is a data processing tool whose input is a digital signal and whose output is its digital spectral analysis. The discrete nature of the DFT yields intrinsic quantization errors and sampling artifacts. This papers addresses the intrinsic errors introduced by the DFT and discusses windowing as a means of error mitigation. Suppose that the sampling rate for digitization is selected to be twice the highest harmonic in the input signal and is denoted by:
The basic idea of (1) is that the DFT spectral analysis will be constrained to range between zero and one-half of the sampling rate. Thus, if the sampling rate is 8,000 Hz, the DFT output will measure frequencies from 0 Hz to 4,000 Hz. Thus, the bandwidth of the DFT is proportional to sample rate. The sampling period,
The kth array element in the frequency domain is referred to as a frequency bucket or bin. Thus we can relate the frequency of bucket k to the frequency of the input signal using:
Equation (3) can also be used to obtain the frequency quantum. The frequency quantum is the change in frequency that is represented by two sequential bucket numbers.For example, suppose that samples, N = 2048, k = 1 and the sample rate is 8000 Hz. Then frequency quantum is 8000/2048 = 3.9 Hz. For k = 0, we have a D.C. component that has zero Hz. Thus, the step between bucket 0 and bucket 1 represents a quantization in frequency. The central point of the spectrum is given by N/2 = 2048/2 = 1024. By (3) we compute the highest frequency that may be represented by 2048 samples (with 8khz sampling rate) as (8000/2048) *1024 = 4000 Hz. Also, we may solve for any sample using: Equation (4) allows us to make two basic assertions about trade-offs in the DFT:
The Heisenberg uncertainty principle states that certain pairs of physical properties cannot be known to arbitrary precision. In the case of quantum physics, the properties are position and momentum. In the case of the DFT, the properties are frequency and time. Thus, we need more samples (that is more time) to get better frequency precision. However, this causes our ability to localize the event (precision in time) to suffer. The converse is also true. As we try to isolate the event in time, the number of samples has declined and so has the precision in frequency. In fact, from (3) we can see that the frequency precision is proportional to the number of samples. Further, we can compute the frequency for any bucket. For example, for a 400 Hz waveform we expect the maximum amplitude to occur at The time-domain rationale for spectral leakage is that, for a waveform that is not periodic in time, the temporal effect of the sample window becomes visible in the Fourier transform [Walker]. Further, if an input signal is finite and the window surrounding the input signal is rectangular then the Fourier transform of the rectangular window is given by the sinc function: 2 WINDOWING"Windowing" amplitude modulates the input signal so that the spectral leakage is evened out (spreading on-bucket signals more and off-bucket signals less). Thus, windowing reduces the amplitude of the samples at the beginning and end of the window, altering leakage. Windowing is implemented by multiplying the input signal with a windowing function. An input signal can be of any number of dimensions and can be complex. For complex-values a complex multiplication is required. For the purpose of simplicity, we assume that the input signal is 1D and real-valued. Windowing functions are also called tapering functions or apodization functions. Apodization is from the Greek and literally means, „removing the feet". It is the technical term for changing the shape of a signal by the use of a function that has a zero-value outside of a selected interval. It involves using a tapering function to smooth out the transitions. There are many common windowing functions. For example, the Hann filter (also called the hanning filter) is named after the Vienese metrologist, Julius Ferdinand von Hann (1839-1921). The Hann window is given by:
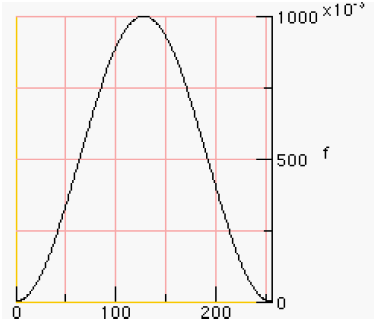
The window falls off at -18 dB per octave. Figure 1 shows the Hann window.
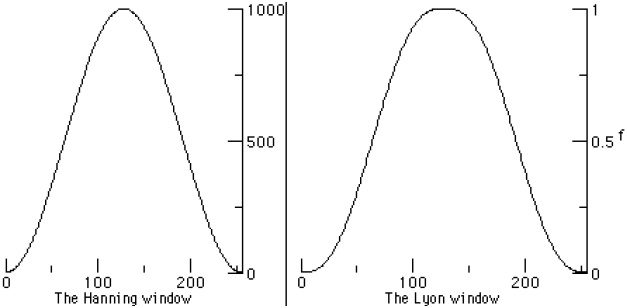
Figure 1. The Hann window The following code graphs the Hann window: The method returns an array of double. To apply the window to the samples, we have devised a windowArray method: The primary difference between one window and the next is the way it tapers off at the ends of the samples. One window, called the Bartlett window, is a linear window that is described by:
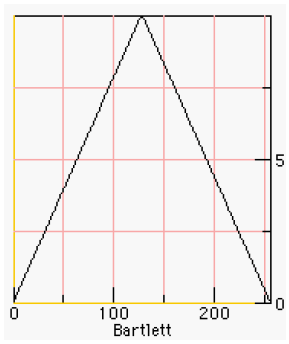
Figure 2. The Bartlett Window Figure 2 shows a graph of a Bartlett window [Bartlett]. The Bartlett window is computed using: 3 A VANITY WINDOWIn this section I create a window, just for fun. Lets call it the Lyon window, first described in [Lyon 1997]. Suppose we start with constraints on a window, then use these constraints to create a polynomial. We propose a window that is zero at the sample end-points and also has zero first and second derivatives at the end-points and the center. Such a window may be formulated with two fifth-order polynomials (two quintics). We present some Maple code for deriving a quintic-based window. Maple is a symbolic manipulator that can help with some math problems. In Maple, we let dy and ddy be the first and second derivatives of the polynomial with respect to the dilation parameter u. The dilation parameter will be varied between zero and one, inclusive. The amplitude of the qunitic will vary from y0 to y1. Maple’s optimize routine can output a procedure for computing quintics in minimum CPU time. What follows is a Maple procedure for generating the Lyon window. See [Lyon 91] for an application of the quintic to maneuvering. We compute the quintic using: The equations for the Lyon window is given by:
The easier way to compute the dilation parameter, u, is by incrementing it by 2/N as in:
Figure 3. The Lyon and Hann windows compared The Lyon and Hann windows are shown in Figure 3. The Lyon window has a flat head (in German, they say "flachem Kopf"), increasing the number of unattentuated samples at the centroid of the event. The flachem kopf windows have zero first and second derivatives at their extrema, thus reducing distortion and "clicks". 4 THE HI-PASS FILTEROne very simple way to design a hi-pass filter is to take an FFT on the input samples, then multiply the spectrum by the filter envelope. For example, to make a hi-pass filter, we may zero out the low frequencies using a rectangular pass-band function, like the one shown in Figure 4.
Figure 4. A passband shown spectral harmonics to admit the PSD
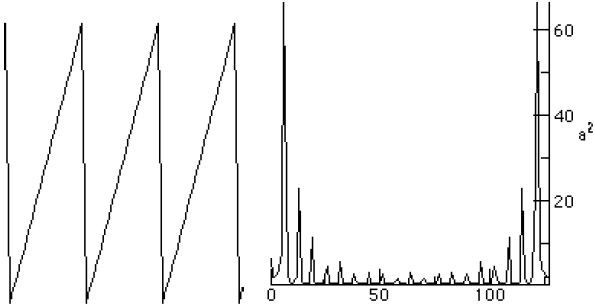
Figure 5. The Saw wave and its PSD
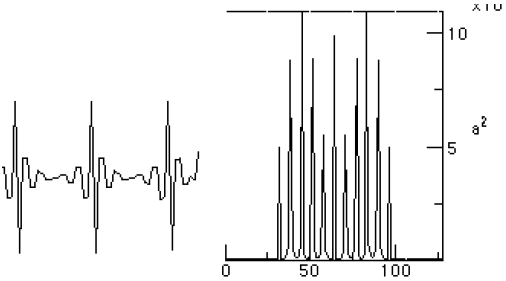
Figure 6. The Hi-pass filtered Saw wave and its PSD For the PSD depicted in this chapter, the higher frequencies are toward the center of the graph. For the determination of the performance of the various windows, we follow [Embree] and plot the windowed waveform along side the log (in dB) of the PSD. We use the dB log and zoom into the first 200 samples of the PSD to make smaller details clear. We compute the graph using:
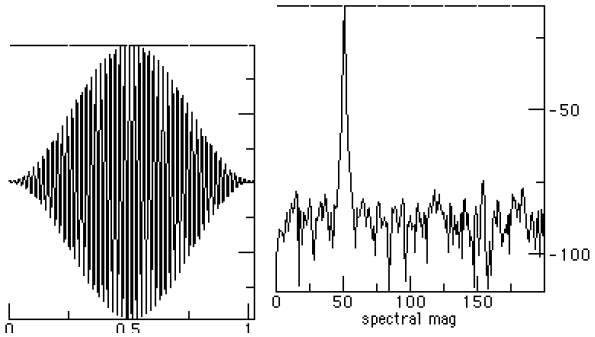
Figure 7. A Rectangular window and spectral dB log. Figure 7 shows a sine wave with a rectangular window. The sine wave is 400 Hz with 8000 Hz sampling. This is often expressed as a relative frequency of 400/8000 = 0.05. Figure 8 shown the Hann window with the spectral log magnitude.
Figure 8. The Hann windowed data with the FFT result. The triangular windowed input of the Bartlett window is shown in Figure 9, along with the PSD.
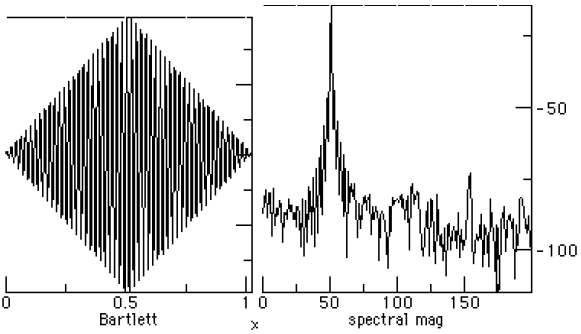
Figure 9. The Bartlett windowed data and the PSD
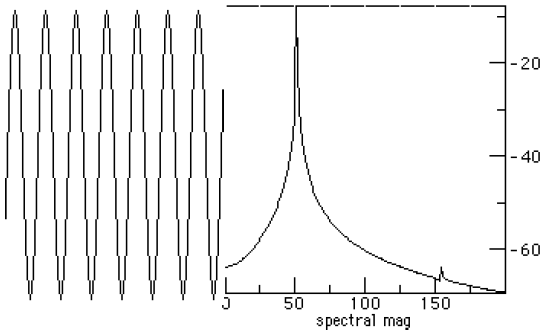
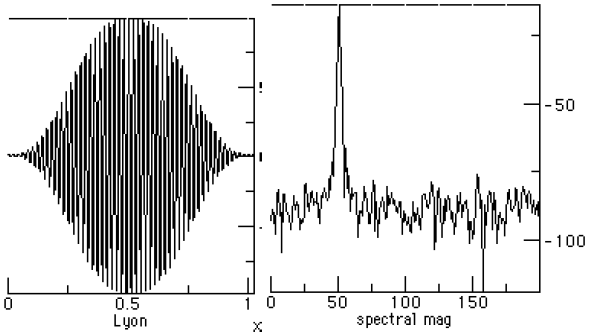
Figure 10. The Lyon window and PSD Figures 9 and 10 show that the Lyon window has somewhat better side lobe performance than the Bartlett window (lower spectral leakage). The main lobe in the Lyon window is narrower than the Bartlett window (lower noise bandwidth). Figure 11 shows the spectra for the Lyon and Hann windows on the left and right, for comparison.
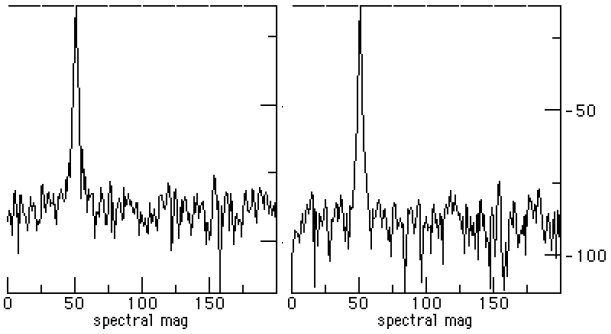
Figure 11. Spectra of Lyon vs. Hann windows The Lyon and Hann windows appear to be spectrally close. The Lyon window appears to have a few dB better side lobe performance over the Hann window. The main lobe is slightly wider, however, and so has a slightly larger equivalent noise bandwidth [Mitra]. 5 SUMMARYWe have seen windowing implemented as the amplitude modulation of a signal by using a finite duration function. The primary goal of windowing is to force the resulting signal to be zero outside of the window range, controlling the transition so that it is not too abrupt. REFERENCES[Arons] "SpeechSkimmer: A System for Interactively Skimming Recorded Speech", by Barry Arons. ACM Transactions on Computer-Human Interaction 4:1, pps. 3-38, 1997. [Bartlett] Bartlett, M. S. "Periodogram Analysis and Continuous Spectra", Biometrika 37, 1-16, 1950. [Embree] C Language Algorithms for Digitial Signal Processing,by Paul M. Embree and Bruce Kimble, Prentice Hall, Englewood Cliffs, NJ, 1991. [Harris] Fredric J. Harris, "On the use of Windows for Harmonic Analysis with the Discrete Fourier Transform", Proceedings of the IEEE, V66N1, Jan. 1978, pp. 51-83. [Lyon 90] "Ad-Hoc and Derived Parking Curves", by Douglas Lyon, SPIE - International Society for Optical Engineering, Boston MA, November 8, 1990. [Lyon 91] Parallel Parking with Nonholonomic Constraints. PhD thesis, by Douglas Lyon, Computer and Systems Engineering Department, RPI, Troy, NY, 12181. Available at http://www.docjava.com, 1991 [Lyon 97] Java Digital Signal Processing, Douglas A. Lyon and H. Rao, M&T Press (an imprint of Henry Holt). November 1997. [Mitra] Handbook for Digital Signal Processing, Sanjit K. Mitra and James F. Kaiser, John Wiley & Sons, NY, NY, 1993. [Walker] Fast Fourier Transforms, James S. Walker. CRC Press, NY, NY, 1996. About the author
Douglas A. Lyon: "The Discrete Fourier Transform, Part 4: Spectral Leakage", in Journal of Object Technology, vol. 8. no. 7, November-December 2009 pp. 23-34 http://www.jot.fm/issues/issue_2009_11/column2/ |
||||||||||
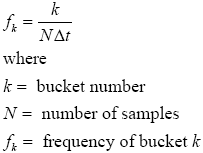 (3)
(3)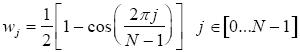 (5)
(5)



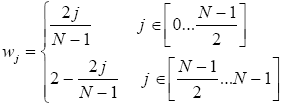 (6)
(6)