|
The Theory of Classification Anthony J.H. Simons, Department of Computer Science, University of Sheffield |
COLUMN PDF Version |
1 INTRODUCTION
This is the first article in a regular series on object-oriented type theory, aimed specifically at non-theoreticians. The object-oriented notion of classification has for long been a fascinating issue for type theory, chiefly because no other programming paradigm has so sought to establish systematic sets of relationships between all of its types. Over the series, we shall seek to find answers to questions such as: What is the difference between a type and a class? What do we mean by the the notion of plug-in compatibility? What is the difference between subtyping and subclassing? Can we explain inheritance, method combination and template instantiation? Along the way, we shall survey a number of different historical approaches, such as subtyping, F-bounds, matching and state machines and seek to show how these models explain the differences in the behaviour of popular object-oriented languages such as Java, C++, Smalltalk and Eiffel. The series is titled "The Theory of Classification", because we believe that all of these concepts can be united in a single theoretical model, demonstrating that the object-oriented notion of class is a first-class mathematical concept!
In this introductory article, we first look at some motivational issues, such as the need for plug-in compatible components and the different ways in which compatibility can be judged. Reasons for studying object-oriented type theory include the desire to explain the different features of object-oriented languages in a consistent way. This leads into a discussion of what we really mean by a type, ranging from the concrete to the abstract views.
2 COMPONENTS AND COMPATIBILITY
The eventual economic success of the object-oriented and component-based software industry will depend on the ability to mix and match parts selected from different suppliers [1]. In this, the notion of component compatibility is a paramount concern:
- the client (component user) has to make certain assumptions about the way a component behaves, in order to use it;
- the supplier (component provider) will want to build something which at least satisfies these expectations;
But how can we ensure that the two viewpoints are compatible? Traditionally the notion of type has been used to judge compatibility in software. We can characterise type in two fundamental ways:
- syntactic compatibility - the component provides all the expected operations (type names, function signatures, interfaces);
- semantic compatibility - the component's operations all behave in the expected way (state semantics, logical axioms, proofs);
and these are both important, although most work published as "type theory" has concentrated on the first aspect, whereas the latter aspect comes under the heading of "semantics" or "model checking". There are many spectacular examples of failure due to type-related software design faults, such as the Mars Climate Orbiter crash and the Ariane-5 launch disaster. These recent high-profile cases illustrate two different kinds of incompatibility.
In the case of the Mars Climate Orbiter, the failure was due to inadequate characterisation of syntactic type, resulting in a confusion of metric and imperial units. Output from the spacecraft's guidance system was re-interpreted by the propulsion system in a different set of measurement units, resulting in an incorrect orbital insertion manoeuvre, leading to the crash [2]. In the case of the Ariane 5 disaster, the failure was due to inadequate characterisation of semantic type, in which the guidance system needlessly continued to perform its pre-launch self-calibration cycle. During launch, the emission of larger than expected diagnostic codes caused arithmetic overflow in the data conversion intended for the propulsion system, which raised an exception terminating the guidance system, leading to the violent course-correction and break-up of the launcher [3]. This last example should be of particular interest to object-oriented programmers, since it involved the wholesale reuse of the previously successful guidance software from the earlier Ariane 4 launcher in a new context.
3 DEGREES OF STRICTNESS AND SOPHISTICATION
How strictly must a component match the interface into which it is plugged? In Pascal, a strongly-typed language, a variable can only receive a value of exactly the same type, a property known as monomorphism (literally, the same form). Furthermore, types are checked on a name equivalence, rather than structural equivalence basis. This means that, even if a programmer declared Meter and Foot to be synonyms for Integer, the Pascal type system would still treat the two as non-equivalent, because of their different names (so avoiding the Martian disaster). In C++, typedef synonyms are all considered to be the same type and you would have to devise wrapper classes for Meter and Foot to get the same strict separation.
Furthermore, all object-oriented languages are polymorphic (literally, having many forms), allowing variables to receive values of more than one type1. From a practical point of view, polymorphism is regarded as an important means of increasing the generality of an interface, allowing for a wider choice of components to be substituted, which are said to satisfy the interface. Informally, this is understood to mean supplying at least those functions declared in the interface. However, the theoretical concept of polymorphism is widely misunderstood and the term mistakenly applied, by object-oriented programmers, variously to describe dynamic binding or subtyping. The usage we shall adopt is consistent with established work in the functional programming community, in that it requires at least a second-order typed lambda calculus (with type parameters) to model formally [4]. However, we must lay more foundations before introducing such a calculus.
A simple approach to interface satisfaction is subtyping. This is where an object of one type may safely be substituted where another type was expected [5]. This involves no more than coercing the supplied subtype object to a supertype and executing the supertype's functions. The coerced object then behaves in exactly the same way as expected. An example of this is where two SmallInt objects are passed to an Integer plus function and the result is returned as an Integer. The function originally expected Integers, but could handle subtypes of Integer and convert them. Note that no dynamic binding is implied or required. Also, a simply-typed first-order calculus (with subtyping) is adequate to explain this behaviour.
We shall call the more complex, polymorphic approach subclassing. This is where one type is replaced by another, which also systematically replaces the original functions with new ones appropriate to the new type. An example of this is where a Numeric type, with abstract plus, minus, times and divide, is replaced by a Complex type, having appropriately-retyped versions of these (as in Eiffel [6]). Rather than coerce a Complex object to a Numeric, the call to plus through Numeric should execute the Complex plus function. Also, there is an obligation to propagate type information about the arguments and result-type of Complex's plus back to the call-site, which needs to supply suitable arguments and then know how to deal with the result. In a later article, we shall see why this formally requires a parametric explanation.
To summarise so far, there are three different degrees of sophistication when judging the type compatibility of a component with respect to the expectations of an interface:
- correspondence: the component is identical in type and its behaviour exactly matches the expectations made of it when calls are made through the interface;
- subtyping: the component is a more specific type, but behaves exactly like the more general expectations when calls are made through the interface;
- subclassing: the component is a more specific type and behaves in ways that exceed the more general expectations when calls are made through the interface.
Certain object-oriented languages like Java and C++ practise a halfway-house approach, which is subtyping with dynamic binding. This is similar to subtyping, except that the subtype may provide a replacement function that is executed instead. Adapting the earlier example, this is like the SmallInt type providing its own version of the plus function which wraps the result back into the SmallInt range. Syntactically, the result is acceptable as an Integer, but semantically it may yield different results from the original Integer plus function (when wrap-around occurs). The selection mechanism of dynamic binding is formally equivalent to higher-order functional programming [7], in which functions are passed as arguments and then are dynamically invoked under program control. So, languages with apparently simple type systems are more complex than they may at first seem.
4 CONCRETE AND ABSTRACT TYPES
How can we explain the behaviour of languages such as Smalltalk, C++, Eiffel and Java in a consistent framework? Our goal is to find a mathematical model that can describe the features of these languages; and a proof technique that will let us reason about the model. To do this, we need an adequate definition of type that will allow reasoning about syntactic and semantic type compatibility. This brings into question what we mean exactly by a type.
Bit-Interpretation Schemas
There are various definitions of type, with increasing formal usefulness. Some approaches are quite concrete, for example a programmer sometimes thinks of a type as a schema for interpreting bit-strings in computer memory, eg the bit-string 01000001 is 'A' if interpreted as a Character; but 65 if interpreted as an Integer. This approach is concerned more with machine-level memory storage requirements than with formal properties necessary to reason about types.
Model-Based and Constructive Types
An afficionado of formal methods (such as Z [8], or VDM) likes to think of types as equivalent to sets:
![]()
This is called the model-based approach, in which the notion of type is grounded in a set-theoretic model, that is, having type (x : T, "x is of type T") is equivalent to set membership
![]()
All program operations can be modelled as set manipulations. The constructive approach [9] also translates a program into a simpler concrete model, like set-theory, whose formal mathematical properties are well understood.
Concrete approaches have their limits [10], for example, how would you specify an Ordinal type? You merely want to describe something that is countable, whose elements are ordered, but not assert that any particular set "is" the set of Ordinals. The set of Natural numbers: Natural = {0, 1, 2...} is too specific a model for Ordinal, since this excludes other ordered things, like Characters, and the Natural numbers are subject to further operations (such as arithmetic) which the Ordinals don't allow (although strictly the set-theoretic model only enumerates the membership of a type and does not describe how elements behave).
Syntactic and Existential Abstract Types
A type theorist typically thinks of a type as a set of function signatures, which describe the operations that a type allows. This characterises the type in a more abstract way, by enumerating the operations that it allows. The Ordinal type is defined as:
![]()
in which ![]() can be read as "let there be an uninterpreted set ord", such that the following operations accept and return elements from this (as yet undefined) set. Ordinal is then defined as the type providing first and succ; and we don't care about the representation of ord. This approach is variously called syntactic, since it is based on type signatures, or existential, since it uses
can be read as "let there be an uninterpreted set ord", such that the following operations accept and return elements from this (as yet undefined) set. Ordinal is then defined as the type providing first and succ; and we don't care about the representation of ord. This approach is variously called syntactic, since it is based on type signatures, or existential, since it uses ![]() to reveal the existence of a representation, but refuses to qualify ord any further.
to reveal the existence of a representation, but refuses to qualify ord any further.
Although syntactic types reach the desired degree of abstraction away from concrete models, they are not yet precise. Consider that the following faulty expressions are still possible:
succ('b') = first() = 'a' - an undesired possibility;
succ(1) = 1 - another undesired possibility;
This is because the signatures alone fail to capture the intended meaning of functions.
Axioms and Algebraic Types
A mathematician considers a type as a set of signatures and constraining axioms. The type Ordinal is fully characterised by:

This form of definition is known as an algebra. Formally, an algebra consists of: a sort (that is, an uninterpreted set, ord, acting as a placeholder for the type); and a set of functions defined on the sort (first, succ), whose meaning is given by axioms. The two axioms (1) and (2), plus the logical rule of induction, are sufficient to make Ordinal behave in exactly the desired way. But how do the axioms work? Let us arbitrarily label: x = first().
- From (1), succ(x)
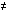 first(), so we know succ(x) is distinct from x; let us choose another arbitrary label: y = succ(x).
first(), so we know succ(x) is distinct from x; let us choose another arbitrary label: y = succ(x).
- From (2) succ(y)
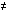 y; from (1) succ(y) * x, so we know succ(y) is distinct from x and y; let us therefore label: z = succ(y) = succ(succ(x)).
y; from (1) succ(y) * x, so we know succ(y) is distinct from x and y; let us therefore label: z = succ(y) = succ(succ(x)).
- From (2) succ(z)
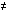 z; from (1) succ(z)
z; from (1) succ(z) 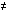 x; but could succ(z) = y? Although there is no ground axiom that instantly forbids this, induction rules it out, because:
x; but could succ(z) = y? Although there is no ground axiom that instantly forbids this, induction rules it out, because:
by substitution of y and z, we get: succ(succ(succ(x))) = succ(x)
by unwinding succ, we get: succ(succ(x)) = x, which is false by (1),
so succ(z) is also distinct; and so on...
Once the algebra is defined, we can disregard the sort, which is no longer needed, since every element of the type can now be expressed in a purely syntactic way:
first(); succ(first()); succ(succ(first())); ...
The algebraic definition of Ordinal says exactly enough and no more [11]; it is both more abstract than a concrete type - it is not tied to any particular set representation - and is more precise - it is inhabited exactly by a monotonically-ordered sequence of abstract objects.
5 CONCLUSION
We are motivated to study object-oriented type theory out of a concern to understand better the notion of syntactic and semantic type compatibility. Compatibility may be judged according to varying degrees of strictness, which each have different consequences. Likewise, different object-oriented languages seem to treat substitutability in different ways. As a preamble to developing a formal model in which languages like Smalltalk, C++, Eiffel and Java can be analysed and compared, increasingly abstract definitions of type were presented. The next article in this series builds on the foundation laid here and deals with models of objects, methods and message-passing.
Footnote
1 Beware object-oriented textbooks! Polymorphism does not refer to the dynamic behaviour of objects aliased by a common superclass variable, but to the fact that variables may hold values of more than one type in the first place. This fact is independent of static or dynamic binding.
REFERENCES
[1] B. J. Cox, Object-Oriented Programming: an Evolutionary Approach, 1st edn., Addison-Wesley, 1986.
[2] Mars Climate Orbiter Official Website, http://mars.jpl.nasa.gov/msp98/orbiter/, September 1999.
[3] J. L. Lions, Ariane 5 Flight 501 Failure, Report of the Inquiry Board, http://sunnyday.mit.edu/accidents/Ariane5accidentreport.html, July 1996.
[4] J. C. Reynolds, Towards a theory of type structure, Proc. Coll. sur la Programmation, New York; pub. LNCS 19, Springer Verlag, 1974, 408-425.
[5] L. Cardelli and P. Wegner, On understanding types, data abstraction and polymorphism, ACM Computing Surveys, 17(4), 1985, 471-521.
[6] B. Meyer, Object-Oriented Software Construction, 2nd edn., Prentice Hall, 1995.
[7] W. Harris, Contravariance for the rest of us, J. of Obj.-Oriented Prog., Nov-Dec, 1991, 10-18.
[8] J. M. Spivey, Understanding Z: a Specification Language and its Formal Semantics, CUP, 1988.
[9] P. Martin-Löf, Intuitionistic type theory, lecture notes, Univ. Padova, 1980.
[10] J. H. Morris, Types are not sets, Proc. ACM Symp. on Principles of Prog. Langs., Boston, 1973, 120-124.
[11] K. Futatsugi, J. Goguen, J.-P. Jouannaud and J. Messeguer, Principles of OBJ-2, Proc. 12th ACM Symp. Principles of Prog. Langs., 1985, 52-66.
About the author
 |
Anthony Simons is a Senior Lecturer and Director of Teaching in the Department of Computer Science, University of Sheffield, where he leads object-oriented research in verification and testing, type theory and language design, development methods and precise notations. He can be reached at a.simons@dcs.shef.ac.uk |
Cite this column as follows: Anthony J. H. Simons: "The Theory of Classification, Part 1: Perspectives on Type Compatibility", in Journal of Object Technology, vol. 1, no. 1, May-June 2002, pages 55-61, http://www.jot.fm/issues/issue_2002_05/column5