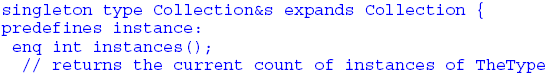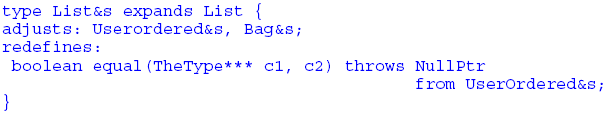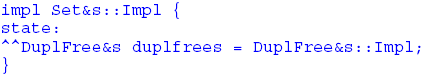Covariantly Adjusting Co-Types in Timor J. Leslie Keedy, Monash University, Melbourne, Australia, University of Newcastle, NSW, Australia and University of Bremen, Germany Gisela Menger, University of Bremen, Germany Christian Heinlein, Aalen University of Applied Sciences, Germany

REFEREED COLUMN PDF Version

Abstract

This paper extends the idea of co-types (described in a companion paper) to include the concept of adjustment hierarchies. An adjustment hierarchy provides a parallel hierarchy to a subtyping hierarchy of a type being expanded by the co-type. This has a number of advantages including the predefinition of co-types for subtypes of an expanded type, and allowing automatic covariant adjustment of parameters for makers, binary methods and instance methods, without creating problems for static type safety.

1  INTRODUCTION

In a companion paper we described the basic concept of co-types and their integration into the Timor programming language [11]. In contrast with most conventional OO languages a Timor type definition consists only of a set of instance methods. It has no constructors, no binary methods and no class (static) methods. It can have several implementations, each of which may implement the type in a different way. An implementation consists of a definition of the instance data, code to implement the instance methods and a single constructor, which can have implementation-oriented parameters. These can vary both in number and type according to the needs of different implementations of the same type.

A co-type expands some other type by providing, as instance methods:

• makers, which can have application-oriented parameters relevant to the initialisation of instances of the expanded type. Makers are invoked by an application to create a new instance of the expanded type.
• binary methods, which have at least two parameters of the expanded type. These function by accessing the instance methods of their parameters as appropriate. Because they are instance methods of a different type, they avoid a number of problems associated with normal binary instance and class methods [2].
• normal instance methods, which can in effect play the role of class methods in other OO languages. The instance data in an implementation of a co-type can likewise play a role similar to that of class data in other OO languages.

In the companion paper we showed that such an arrangement helps to deal with problems which would otherwise arise in a language such as Timor, because of its support for multiple implementations of a type and qualifying types with bracket methods.

We pointed out that a co-type can have subtypes, provided that these expand the same type as their supertype. We also drew attention to the fact that while subtypes of a co-type cannot expand subtypes of its expanded type, a close relationship nevertheless exists between subtype hierarchies of an expanded type and co-types for these subtypes. This paper describes the relationship between these hierarchies in the context of Timor. In doing so, we present a new concept, which we call adjustment. This mechanism allows co-type definitions and their implementations to serve as a pattern for co-types of subtypes of an expanded type and their implementations.

We also introduce a safe form of automatic covariant adjustment of the parameters of co-types, to reflect the different expanded types which occur in the subtype hierarchy of the initial expanded type. Thus for example in a Person hierarchy with subtypes Student and Employee, makers and/or binary methods appearing in a co-type for Person can optionally be adjusted automatically to serve as makers/binary methods for Student or Employee. This approach potentially spares the programmer from writing such methods explicitly and helps to ensure consistency between co-types which are related via an adjustment hierarchy.

Section 2 describes the aims of the adjustment concept in a general way. Section 3 introduces an example of a type hierarchy. Section 4 presents binary methods for a normal co-type and shows how similar binary methods can appear in co-types for subtypes of the expanded type. Section 5 uses this example to illustrate the idea of covariantly adjustable parameters. Sections 6 and 7 extend the idea to makers and to co-type instance methods. In section 8 it is shown how adjusted co-types are derived and can be modified. Sections 9 and 10 illustrate the reuse of code in adjustment hierarchies. A section then follows on related work and after that a conclusion.

2  THE AIMS OF ADJUSTMENT

An adjustment hierarchy consists of co-types that mirror a subtype hierarchy for an expanded type. Given a subtype hierarchy consisting of a root type Person with two subtypes Student and Employee (see Figure 1), an adjustment hierarchy could be created (cf. Figure 2), where Persons expands Person, Students expands Student and Employees expands Employee.

Figure 1: A subtype hierarchy	Figure 2: An adjustment hierarchy

Adjustment hierarchies preserve some features of inheritance without generating a subtype relationship.

Several advantages can accrue from this concept.

1. Input parameters (and of course return types) in the corresponding methods of an adjustment hierarchy can be safely changed covariantly.
2. An adjustment hierarchy can help the co-type designer to ensure that all cases are covered, because it provides a systematic approach which allows methods to be predefined, and these are available even for subtypes which are added later in the subtype hierarchy. Thus if a type Manager is added as a subtype of Employee, then by definition a co-type Managers appears in the adjustment hierarchy under Employees. This is particularly helpful when co-types are designed as components which can be added to different systems.
3. For the application programmer the existence of an adjustment hierarchy can guarantee that where certain methods exist in a co-type for an expanded type, similar methods will exist in co-types for all the subtypes of the expanded type.
4. Implementations of co-types can be re-used in implementations of other co-types in the adjustment hierarchy.

Here are some of the differences between a subtype hierarchy and an adjustment hierarchy, as illustrated from Figures 1 and 2:

• Whereas Student and Employee are subtypes of Person, Students and Employees are not subtypes of Persons. Thus an instance of type Student can be assigned to a variable of type Person, but an instance of type Students cannot be assigned to a variable of type Persons.
• A co-type functions only for its corresponding expanded type. Thus Students cannot act as a co-type for Person or Employee.
• Whereas a subtype hierarchy is open-ended and is extended explicitly, an adjustment hierarchy has a parallel set of nodes corresponding to those in the subtype hierarchy, starting at the node where a new co-type is explicitly defined.
• Because co-types in an adjustment hierarchy are not subtypes of their adjusting ancestors, methods in a higher level co-type need not appear in corresponding lower level co-types.
• Since any type can serve as an expanded type for a new co-type, it is possible for example to define an additional co-type Students2 for Student, and co-types derived by adjustment from Students2 will not apply to Person or Employee or their subtypes, but only to subtypes of Student.

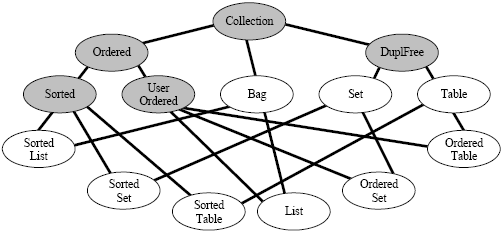
The terminology "adjusting" and "adjusted" are used in this paper to indicate co-types and methods which have an adjustment relationship to each other. The ancestor(s) and the children of a co-type in the adjustment hierarchy is/are called its predecessor(s) and its successor(s).

We now consider a subtype hierarchy and show how an adjustment hierarchy for this might appear.

3  AN EXAMPLE - THE TIMOR COLLECTION LIBRARY

The Timor Collection Library (TCL) is a subtype hierarchy based on an abstract type Collection. An outline of the TCL was first presented in an earlier paper [8], which in some respects is now superseded by the concept of co-types as presented in this and the companion paper. In this section we draw liberally on the example as presented in the earlier paper.

Following a collection concept developed initially for Collja [4, 12, 13], the TCL defines the organisation of general collections according to the following orthogonal properties of their elements:

• duplication of elements in three forms:
  • duplicates are allowed,
  • duplicates are ignored,
  • duplicates are signalled as exceptions.
• ordering of elements in three forms:
  • unordered,
  • user-ordered,
  • sorted by user-defined criteria.

The TCL thus has nine concrete collection types, reflecting all the combinations of these properties. These are as follows:

To facilitate their polymorphic use with a high degree of flexibility there are also five abstract nodes:

• the root type Collection (which serves as a polymorphic supertype for all collections);
• the type DuplFree (derived from Collection, a polymorphic supertype for all collections which may not contain duplicate elements),
• the type Ordered (derived from Collection, a polymorphic supertype for all ordered collections),
• the type UserOrdered (derived from Ordered, a polymorphic supertype for all user ordered collections) and
• the type Sorted (derived from Ordered, a polymorphic supertype for all sorted collections).

The complete structure is illustrated in Figure 3.

Figure 3: Structure of the Timor Collection Library

In order to guarantee behavioural conformity all the common methods of all collection types are initially defined in Collection with a maximum of behavioural flexibility. Thus its (abstract) me­thod insert, for example, does not define

• how an insertion affects the ordering of the collection,
• whether the insertion will be successful if it involves inserting a duplicate,
• whether an exception will be thrown to indicate a duplicate (but it defines an exception DuplEx which might be thrown).

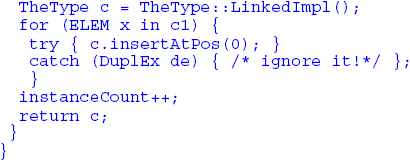
An abstract type with such methods is designed to allow a maximum of polymorphism. In derived types the actions of the insert method are specified more precisely, depending on the node in question. Thus the insert method of the abstract type UserOrdered defines that insert appends the element at the end of the collection (and adds new methods for inserting at other positions) but without defining its duplication properties further. On the other hand the insert method of the concrete type Bag is defined without specifying ordering, but indicating that duplicates are accepted (with the effect that the exception DuplEx can be removed from Bag's insert method). The actual definitions of all the methods of Collection and its subtypes are not important in the present context.

4  BINARY METHODS

We now define a co-type which expands Collection with binary methods.

This co-type does not include makers, because its expanded type Collection is abstract and therefore cannot be instantiated. However the co-type is a concrete type which provides a binary method for comparing concrete collection instances. The actual concrete types of the collections being compared are not important (provided that they are subtypes of Collection), because the comparisons are made ignoring the order (if any) of the elements. Similarly, because the comparison is made element by element it is not important how the actual collections are individually defined with respect to duplicates. (Notice also that the actual collections being compared can have different implementations, since the binary methods invoke the instance methods of their parameters to make the comparisons.)

Similar binary methods can be defined which use different criteria to make the comparisons. The Collection hierarchy provides an excellent pattern for defining these. For example, expanding the type Ordered results in the following co-type:

Notice that in this case also, actual collections of different types can be compared, provided that they are subtypes of Ordered.

The following example compares concrete collections of the type Sorted­Set:

5   ADJUSTING PARAMETERS COVARIANTLY IN TIMOR

Each of the co-types defined above follows a similar pattern (in its definition), though in these examples the input parameters differ according to the type being expanded. For this reason it would not be safe to define them in a normal subtyping relationship.

The following co-type definition can form the basis for an adjustment hierarchy which has a co-type for each of the Collection subtypes. We have introduced three syntactic features which allow such a hierarchy to be defined.

Since each co-type in an adjustment hierarchy is a separate type, it needs its own type identifier, and for all the successors of the highest node the identifier has to be created automatically. In order to achieve this, the type name of each adjusting co-type has three parts: the name of the expanded type (here Collection), the ampersand character (&) and a suffix (here s).

The names of adjusted co-types then consist of the appropriate subtype name, the ampersand character, and the same suffix, e.g. Ordered&s, List&s.

The ampersand character is not permitted in identifier names in Timor except in this context. This character signals that the co-type is part of an adjustment hierarchy. Several adjusting co-types can be created for the same expanded type, using different suffixes and co-types can be defined using normal identifiers, but the latter do not generate adjustment hierarchies.

The methods which must appear in each successor are listed in a section where the section name (here binary) is preceded by the keyword predefines.

The keyword TheType, which is not limited to predefining sections, indicates where covariant parameter adjustment takes place. In each individual co-type in the adjustment hierarchy the name of the corresponding expanded subtype is implicitly substituted for this keyword.

Although the use of TheType allows signatures for similar methods to be automatically generated, the methods themselves may need to be redefined in terms of their functionality and/or may need individual implementations.

6  COVARIANT MAKERS

We omitted makers from the co-type Collections (and the above version of Collection&s), because their expanded type Collection is an abstract type, which cannot therefore be instantiated.

However, introducing adjustment allows makers to be predefined in a co-type for an abstract type, such that these only become run-time methods in co-types for its concrete subtypes. To achieve this we simply predefine makers in an analogous way to the predefinitions of binary methods.

We change the example of Collection&s to include predefined makers:

Notice that the input parameter of the maker convert is not defined as covariantly adjustable. The reason is that it should be possible to create an instance of a specific collection type from instances of any subtypes of Collection, e.g. by merging them in such a way that the resulting order and duplication properties conform to the definition of the expanded type. This technique allows an instance of any concrete collection type to be converted (by copying the relevant elements) to an instance of any other concrete collection type.

7  INSTANCE METHODS

Instance methods of co-types can have parameters of the expanded type, and in this case parameters declared as TheType are adjusted covariantly in adjusted successor co-types.

Instance methods of co-types which play a role similar to that of class methods in conventional OO languages typically do not have parameters of the expanded type. Nevertheless it can make sense to provide these as predefined methods, even in cases where the expanded type is an abstract type. For example each co-type might maintain a count of the number of instances which its makers have created. Then each co-type could provide an instance method which returns the value of the count.

In this example the keyword predefines ensures that an appropriate instance method would exist in each co-type in the hierarchy. Timor ensures that singleton types have only one instance within a persistent file, see [11].

Instance Methods which are not Predefined

In this case the makers for concrete subtypes of Collection would call the method and then initialise the newly created collection with the serial number. The method is not predefined, because only the singleton object instantiated from Collection&s would control the issuing of serial numbers.

Protected Methods and Co-type Hierarchies

As the above example illustrates, co-types can define protected methods as a mechanism by which controlled access is provided for other co-types in the same adjustment hierarchy.

8  DEFINING ADJUSTMENT HIERARCHIES

This section describes how successor co-types in an adjustment hierarchy can be defined in a manner analogous to the definition of subtypes in a conventional object oriented programming language, modifying the syntax for Timor's derived types where appropriate.

An Example Definition of Collection&s

We begin by drawing together the previous examples to provide an overview of a co-type Collection&s, which includes a subset of the methods provided in the TCL. This serves as starting point for illustrating the principles of adjustment.

This example automatically implies that co-types, which have the same predefining methods, exist for all the subtypes of Collection, and that these have names such as Bag&s, List&s, etc. These can be used without being explicitly defined, unless the programmer needs to make explicit modifications to the predefined methods or add new methods (which can but need not) be predefining.

Explicitly Modifying Implicit Co-Type Definitions

• To make changes to an implicit successor co-type the programmer provides an explicit definition of this which is introduced with the keyword adjusts (in an analogous way to the use of extends or includes for defining derived types in Timor [10, 9, 8, 7]).
• Methods with semantics which need to be redefined are explicitly described in a redefines section and in the adjusted co-type these replace the corresponding methods from the adjusting type, provided that the signature does not change (analogous to "overriding"). Changes involving only the meaning of TheType are not considered to be changes in this sense, and therefore require no redefinition.
• New methods can be added in the usual way in appropriate sections. If a new method is defined which has the same identifier as that of a predefined method but with a changed signature (other than changes involving only the meaning of TheType) then this method is considered to be a new method (analogous to “overloading”). In this case both the predefined method and the new method are present in the adjusted type.
• Where signatures of predefined methods need not be changed (except for covariant adjustments), neither the relevant section nor its methods need (but can) be included in the redefinition of the co-type.

Redefining Co-Type Methods: An Example

The binary method in this example needs a semantic redefinition in the co-type for ordered collections. Here is an extract illustrating this.

Adding New Methods: An Example

A key difference between UserOrdered&s and its predecessor Ordered&s is that it introduces a new maker which creates a new collection that has the reverse order of its parameter, i.e.

Notice that a reverse operation cannot be defined in Ordered&s because there is no reversal order which can produce a sorted collection (because these are ordered according to explicitly provided sorting criteria which affect the type definition). However, a sorted collection can be reversed, in which case it becomes a user-ordered collection. Unordered collections cannot be reversed, as they have no order.

Merging of Multiply Adjusted Co-Types for Diamond Inheritance

When an expanded type has two or more supertypes (as in the case of most of the concrete types in the collection hierarchy) the question of merging the corresponding adjusted co-types arises. This issue resembles that which arises in a subtyping hierarchy with diamond inheritance and is handled in an analogous way (see [8]).

Type Adjustment Rule 1: If in an adjusted type multiple methods which result from a common adjusting predecessor and which have the same signature (in this context including parameters defined using the keyword TheType), they are treated as a single method (unless they have return types which differ from each other, in which case a compile time error arises). According to this definition makers, binary methods and instance methods can all be merged.

Type Adjustment Rule 2: If the definitions of such methods differ (i.e. if one or more of them has been redefined differently from the definition in their closest common predecessor), they must also be listed in a redefines clause in the type being defined.

Rule 2 in effect requires that conflicting definitions are clarified. Where a definition in one of the ancestors can be used in the new type this can be signalled by the use of the keyword from followed by the name of the appropriate co-type.

For example List&s is adjusted from both UserOrdered&s and Bag&s. One of the methods which it derives from both is the binary method equal, which can be redefined as follows:

Merging of Multiply Adjusted Co-Types for Parts

Lack of space prevents us from providing a detailed description of co-types for types which result from the multiple inheritance of separate types. However, the principles basically follow mutatis mutandis those used in defining the types themselves (see [9]). In the co-type the keyword adjusts is used instead of extends or includes, and in the case of repeated inheritance multiple co-type methods for a repeated expanded type are not required.

9  IMPLEMENTING ADJUSTMENT HIERARCHIES

In accordance with the normal Timor implementation approach [10, 8] any type (including a co-type) can have different implementations coded in different ways. Code is inherited neither in implementations of subtypes nor in successor co-types, and like any other type, these can be implemented from scratch. The only relationship which might exist between implementations of related types is via re-use variables. However re-use variables can also, where appropriate, be based on implementations of types which are unrelated to the type which is currently being implemented [6, 9]¹.

As at the type level, the keyword TheType can appear anywhere in the code of a co-type implementation as if it were the name of the expanded type of the co-type currently being implemented. The keyword predefines is not used in implementations, because the compiler does not automatically produce adjusted implementations of successor co-types.

We illustrate an implementation of Collection&s and then show how this can be re-used to implement successor co-types.

An Example Implementation of Collection&s

For illustration purposes the makers in this example return a linked implementation of the corresponding expanded Collection type. (An algorithm which chooses between different implementations of the expanded type could of course be used, but this would unnecessarily complicate the example.)

Implementing the Successor Co-Types

We now try to use the normal Timor re-use variable technique (see [6, 9]) in an attempt to implement Bag&s. Our first attempt might be along the follow lines:

The methods of Collection&s match those of Bag&s, and in principle the implementations require no changes, since neither new methods nor code overriding is required. However in the process of matching the methods of Collection&s to those of Bag&s a type problem arises because the relevant parameters have not been covariantly adjusted.

To overcome this problem we extend the idea of re-use variables to take covariant adjustment into account, and to make this clear such re-use variables are denoted by a double hat symbol, as follows

To achieve the adjustment each use of TheType in Collection&s::Impl is adjusted to the expanded type of the current implementation, i.e. in this case each occurrence of TheType is treated as if it means Bag.

The expanded type Bag is a concrete type, but Collection&s::Impl was framed in such a way that no further change is necessary. In fact the following further co-types could be implemented in a similar way:  DuplFree, Set, Table. However, all three could be more efficiently implemented, e.g. as follows:

In this case we have simply "overridden" the equal method from Collection&s with more efficient code. (There is no confusion with matching, since a method which is explicitly re-implemented results in a non-match with the re-use variable.) But now Set&s (and Table&s) could be implemented as

Implementing the Co-Types for Ordered Collections

The same principles can easily be applied to Ordered&s and its successors, where in this case the ordering of elements is important for the binary method equal.

This co-type implementation could, for example be re-used in UserOrdered&s, which also needs an additional maker, e.g.

Handling Multiple Predecessors

In this example some co-types have multiple predecessors. In principle it would be possible to nominate multiple re-use variables (which could be relevant for cases involving parts inheritance [9]), but in this example it is not necessary to do so. For example List&s has two predecessors, but its implementation can simply re-use UserOrdered&s.

Alternative Implementations

As we demonstrated for example in [8] the way in which re-use variables are applied need not follow a pattern similar to subclassing. It would for example be equally feasible to begin the implementations with an implementation of List&s and re-use this to implement the other co-types in the TCL.

10 FURTHER CODE RE-USE TECHNIQUES

The techniques described previously can result in very significant savings both at the type and implementation levels. However, they do not illustrate how the code of predecessor co-types can be re-used in cases where methods are not predefined.

Suppose that a type Person has been defined with three abstract variables name, address and dateOfBirth. A co-type Persons might expand Person by defining a maker init with parameters for initialising the three abstract variables and a binary method equal which compares the values of the three abstract variables. It is not intended that successor co-types should have exactly equivalent makers or binary methods and therefore these are not declared as predefining. As we shall see it can nevertheless help with re-use if the methods are coded in terms of TheType:

Here is an implementation of Persons:

A type Student might extend Person by adding two abstract variables uniName and matricDate and this could have a co-type Students which defines a maker with parameters for initialising both Person-related and Student-related variables. A binary method might compare the values of all five abstract variables. The co-type for Student is not adjusted from Persons. We use different method names to emphasize this.

Because Persons is defined in terms of TheType an implementation of Students could re-use an implementation of Persons as follows:

Thus Students::Impl re-uses the code of Persons::Impl in order to initialise/compare the Person details and then adds further code to initialise/compare the Student details. Notice that in this context any implementation of Persons could be re-used.

In summary, although the methods of a co-type may not be predefining (nor even have the same names) the modified re-use technique can be applied to good effect to re-use the co-type in implementations of related co-types.

11 RELATED WORK

Co-type adjustment represents a limited form of covariant parameter adjustment as found for example in Eiffel [15, 14]. This technique has fallen into disrepute because in the case of input parameters² it can lead to breaches of static type safety in connection with subtyping (cf. [3, 16, 17]).

Bruce et al. [2] examined this issue with respect to binary methods in considerable detail. The essence of their discussion is that covariant adjustment of parameter types cannot be fully reconciled with inheritance, that there can be a loss of symmetry and that privileged access to the code of one binary parameter can be lost. In the Timor philosophy privileged access is not encouraged, because we see it as a violation of the information hiding principle. It will be evident to readers that Timor treats binary method parameters symmetrically in co-types, albeit not in the sense of Bruce et al.

More significantly, by defining binary methods as instance methods in co-types Timor side-steps the issue of reconciling covariant adjustment with inheritance. This separation makes covariance possible in an adjustment hierarchy (not only for binary methods but also for makers and instance methods), leaving the possibility of subtype polymorphism open not only for expanded types but also (independently) for co-types, provided that they expand the same type. Hence all the aims formulated by Bruce et al. are reconciled in Timor, albeit in an unconventional way.

The benefits of covariant input parameters for binary methods can be partly achieved via overloading, e.g. with Java and C++. When overriding inherited methods the number and types of input parameters must be retained unchanged, but the same-named methods with covariant parameter types can be added in subtypes. However, using this possibility can easily lead to confusion, if attention is not paid to the fact that the selection of the fitting method at compile-time depends on the statically declared types of the objects involved. Therefore explicit type conversions may be necessary to ensure that the desired methods will be called. Type checks and type conversions at run-time are inevitably incurred when overriding an inherited binary method, but using overloaded methods instead does not always eliminate these. Overloading the Java equals-methods for example is not recommended, because it is considered costly and error-prone (see [1] pp.26-35). By contrast the Timor approach simplifies the programmer's task and avoids additional run-time checks.

Finally, in his PhD thesis [16] Schmolitzky proposed avoiding a further problem with binary class methods which arises as a result of static binding, by allowing the equivalent of Timor's TheType to be used to select, for example, the appropriate equal method dynamically, i.e. by using a syntax which in Timor might look like TheType.equal(p1, p2). However, because Timor co-types do not use static binding, this problem does not exist and therefore Timor does not support this use of TheType.

12  CONCLUSION

The paper builds on the concept of co-types described in a companion paper [11], adding the idea that co-types can be enhanced in a new hierarchical arrangement which superficially resembles subtyping but which has some crucial differences. The basic idea of an adjustment hierarchy is that the definitions and implementations of makers, binary methods and instance methods (corresponding to static methods in conventional class based languages) for expanded types can be adjusted covariantly to match the subtyping hierarchy of the expanded types without creating problems for static type safety. Some of the additional advantages of this technique are as follows.

Using adjustment hierarchies can help the co-type designer to ensure that all cases are covered, because they provide a systematic approach by predefining methods. The implementer of a hierarchy can also take advantage of implementations of other co-types in that the compiler can automatically adjust re-use variables covariantly.

For the application programmer using co-types an adjustment hierarchy guarantees that certain makers, binary methods and instance methods (i.e. those which are predefined) exist in co-types for all the types in a subtype hierarchy.

From the technical viewpoint covariant adjustment can be used not only for return types but also for input parameters in a type safe manner.

Over and above this, the idea of co-types as such is very useful, providing a modular basis on which types and their co-types can be expanded in different ways, allowing them to be designed and implemented as separate components by software houses and even to be concurrently used in a single system, in contrast with the conventional idea of supporting a single hidden "class object" associated with each class.

Finally we note that adjustment hierarchies (and all their advantages) can be used not only where the expanded type has a hierarchy of subtypes, but also where expanded types are derived by inclusion and therefore do not have a subtyping relationship [10].

Footnotes

1 The re-use variable technique is related to delegation, but is more efficient. If the types of re-use variables have interface methods which match those of the type being implemented, then the corresponding method implementations are treated as the required implementations, unless the method is explicitly re-implemented. A re-use variable can also be used like any other internal variable.

2 Covariant changes to return types were added to the 1998 version of C++ and to the 2005 version of Java, because this does not create breaches of static type safety.

REFERENCES

[1] J. Bloch, Effective Java, Addison-Wesley, Boston, 2005.

[2] K. B. Bruce, L. Cardelli, G. Castagna, The Hopkins Objects Group, G. T. Leavens and B. Pierce, On Binary Methods, Theory and Practice of Object Systems, 1 (1995), pp. 221-242.

[3] W. R. Cook, A Proposal for Making Eiffel Type-safe, The Computer Journal, 32 (1989), pp. 305-311.

[4] M. Evered and G. Menger, Very High Level Programming with Collection Components, 29th international Conference on Technology of Object-Oriented Languages and Systems, Nancy, 1999, pp. 361-370.

[5] J. L. Keedy, K. Espenlaub, C. Heinlein and G. Menger, Persistent Objects and Capabilities in Timor, Journal of Object Technology, 6 (2007), pp. 103-123 http://www.jot.fm/issues/issue_2007_05/article3/.

[6] J. L. Keedy, C. Heinlein and G. Menger, Reuse Variables: Reusing Code and State in Timor, 8th International Conference on Software Reuse, Springer Verlag, Berlin, Madrid, 2004, pp. 205-214, http://www.springerlink.com/content/vh35l5ulhhmyk39x/?p=bac45e4a92a2433f9a6bb13aad40781b&pi=12.

[7] J. L. Keedy, G. Menger and C. Heinlein, Diamond Inheritance and Attribute Types in Timor, Journal of Object Technology, 3 http://www.jot.fm/issues/issue_2004_11/article2/ (2004), pp. 121-142,

[8] J. L. Keedy, G. Menger and C. Heinlein, Inheriting from a Common Abstract Ancestor in Timor, Journal of Object Technology, 1 (2002), pp. 81-106, www.jot.fm/issues/issue_2002_05/article2/.

[9] J. L. Keedy, G. Menger and C. Heinlein, Inheriting Multiple and Repeated Parts in Timor, Journal of Object Technology, 3 (2004), pp. 99-120, http://www.jot.fm/issues/issue_2004_11/article1/.

[10] J. L. Keedy, G. Menger and C. Heinlein, Support for Subtyping and Code Re-use in Timor, in J. Noble and J. Potter, eds., 40th International Conference on Technology of Object-Oriented Languages and Systems (TOOLS Pacific 2002), Conferences in Research and Practice in Information Technology, Sydney, Australia, 2002, pp. 35-43.

[11] J. L. Keedy, G. Menger and C. Heinlein, Types and Co-Types in Timor, (2009), in Journal of Object Technology, vol. 8, no. 7, November-December 2009, pp 39-58, http://www.jot.fm/issues/issue_2009_11/column4/

[12] G. Menger, Unterstützung für Objektsammlungen in statisch getypten objektorientierten Programmiersprachen (Support for Object Collections in Statically Typed Object Oriented Languages), Ph.D.Thesis, Dept. of Computer Structures, University of Ulm, Germany, 2000.

[13] G. Menger, J. L. Keedy, M. Evered and A. Schmolitzky, Collection Types and Implementations in Object-Oriented Software Libraries, 27th International Conference on Technology of Object-Oriented Languages and Systems, Santa Barbara CA, 1998, pp. 97-109.

[14] B. Meyer, Eiffel: the Language, Prentice-Hall, New York, 1992.

[15] B. Meyer, Object-oriented Software Construction, Prentice-Hall, New York, 1988.

[16] A. Schmolitzky, Ein Modell zur Trennung von Vererbung und Typabstraktion in objektorientierten Sprachen (A Model for Separating Inheritance and Type Abstraction in Object Oriented Languages), Ph.D. Thesis, Dept. of Computer Structures, University of Ulm, Germany, 1999.

[17] A. Schmolitzky, M. Evered, J. L. Keedy and G. Menger, How can Covariance in Pragmatical Class Methods be made Statically Type-safe, 32nd International Conference on Technology of Object-Oriented Languages and Systems (TOOLS Pacific 1999), IEEE Computer Society 1999, ISBN 0-7695-0462-0, Melbourne, Australia, 1999, pp. 200-209.

About the author

		J. Leslie Keedy retired from the position of Professor and Head, Department of Computer Structures, University of Ulm, Germany in 2005, where he previously led the Timor language design and the Speedos operating system design groups. His email address is keedy@jlkeedy.net. His biography can be visited at http://www.jlkeedy.net/biography_short.php
		Christian Heinlein is Professor for Fundamentals of Computer Science and Software Engineering at Aalen University, Germany. In his research, he has developed "Advanced Procedural Programming Languages", which are both conceptually simpler and more flexible than standard object-oriented languages. More information about him and his work can be found at www.htw-aalen.de/personal/christian.heinlein.
		Gisela Menger received a Ph.D. in Computer Science from the University of Ulm in 2000. She recently retired from the Department of Computer Structures at the University of Ulm. Her research interests include programming language design and software engineering.

J. Leslie Keedy, Gisela Menger, Christian Heinlein: "Covariantly Adjusting Co-Types in Timor", in Journal of Object Technology, vol. 9, no. 1, January-February 2010, pp 35-55 http://www.jot.fm/issues/issue_2010_01/column4/